Πηγή: Καταλήψεις-Αναπλήρωση μαθημάτων – Τηλεκπαίδευση και απουσίες 2024
Μήνας: Ιανουάριος 2024
ΕΥΚΛΕΙΔΗΣ 2023-24
Introduction to Probability for Data Science
Stanley H. Chan
An undergraduate textbook on probability for data science.
Συνεργασία και Συναγωνισμός
Πρoστατευμένο: Γεωμετρικοί Μετασχηματισμοί I.Yaglom
omilos1021b10122021 Δύναμη Σημείου ως προς κύκλο και άλλα προβλήματα
Θεωρία Παιγνίων Βιβλίο
Εισαγωγή στα Μαθηματικά
Everything You Always Wanted To Know About Mathematics*
https://www.math.cmu.edu/~jmackey/151_128/bws_book.pdf
bws_bookΌλοι οι τριγωνομετρικοί αριθμοί στον τριγωνομετρικό κύκλο
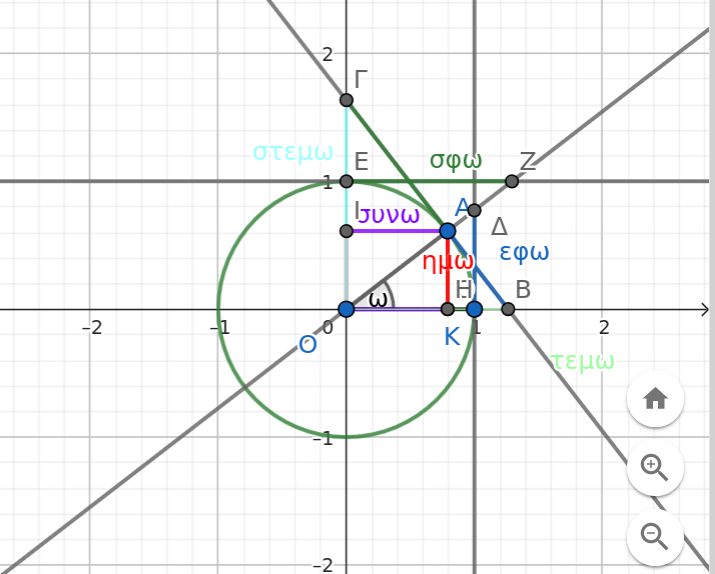
Δείτε και εδώ: https://www.geogebra.org/calculator/pra4xees
Εμφανίστε σε πλήρη οθόνη το παρακάτω, μετακινώντας προς τα κάτω τα βασικά εργαλεία και εμφανίζοντας το

Σύντομη ιστορία τριγωνομετρίας:
Θέματα ΕΥΚΛΕΙΔΗ Β-Γ λυκείου με λύσεις από www.mathematica.gr
Να λυθεί η εξίσωση \( \frac{3}{x-1} + \frac{2}{x-2} + \frac{1}{x-3} = 3 \)
Θεωρούμε το τριώνυμο \( f(x)=4x^2 +kx + m \) και υποθέτουμε ότι οι ρίζες του είναι
διακεκριμένες και ανήκουν στο διάστημα (0,1) . Να αποδειχθεί ότι τουλάχιστον ένας
από τους \( k, m \) δεν είναι ακέραιος
Αν οι θετικοί πραγματικοί αριθμοί \( a, b \) ικανοποιούν τη σχέση:
\[ \frac{a}{b+a} + \sqrt[3]{\frac{b}{a}} = \frac{3}{2} \]
να αποδειχθεί ότι: \( a = b \).
Να βρεθεί ο μεγαλύτερος θετικός ακέραιος \( k \) με την ακόλουθη ιδιότητα: Ο αριθμός 2018
γράφεται ως άθροισμα \( k \) τετραγώνων διαφορετικών ακεραίων.
Πρόβλημα 2
Έστω \( a_1 , a_2 , a_3 , … , a_7 \) θετικοί ακέραιοι που είναι διαδοχικοί όροι αριθμητικής
προόδου. Δίνεται επίσης ότι το άθροισμά τους είναι τέλειος κύβος και το άθροισμα
των 5 μεσαίων όρων \( a_2 , a_3 , a_4 , a_5 , a_6 \) είναι τέλειο τετράγωνο. Να βρεθεί η ελάχιστη
δυνατή τιμή του όρου \( a_4 \) .

