Μήνας: Οκτώβριος 2021
Πολλές ρίζες και δυνάμεις…
Η ανισότητα Cauchy-Schwarz από την ανισότητα Αριθμητικού – Γεωμετρικού μέσου
Η ανισότητα Αριθμητικού – Γεωμετρικού μέσου
Ο Αριθμητικός μέσος δύο ή περισσοτέρων αριθμών είναι το άθροισμά τους προς το πλήθος τους: \( \frac{a+b}{2} , \frac{a+b+c}{3},\ldots , \frac{a_1 + a_2 + \cdots + a_n}{n}\)
ενώ ο γεωμετρικός μέσος αφορά στο γινόμενό τους: \( \sqrt{ab}, \sqrt[3]{a\cdot b \cdot c}, \ldots , \sqrt[n]{a_1 \cdot a_2 \cdots a_n}\)
όσο είναι το πλήθος των αριθμών είναι και η τάξη της ρίζας και προφανώς θα ορίζεται για μη αρνητικούς αριθμούς.
Συνδέονται μεταξύ τους με την ανισότητα: \(\sqrt{ab} \leq \frac{a+b}{2}\)
και γενικεύοντας για n το πλήθος όρους έχουμε: \(\sqrt[n]{a_1 \cdot a_2 \cdots a_n} \leq \frac{a_1 + a_2 +\cdots + a_n}{n}\)
Απόδειξη για δύο όρους
Έχουμε ήδη δει απόδειξη για δύο όρους στα προηγούμενα, η οποία ανάγεται στη βασική ιδιότητα των πραγματικών αριθμών \(a^2 \geq 0 \) .
Συγκεκριμένα για κάθε \( a,b \geq 0\) έχουμε διαδοχικά: \(\sqrt{ab} \leq \frac{a+b}{2} \Leftrightarrow 2 \sqrt{ab} \leq a+b \Leftrightarrow 4ab \leq a^2 + b^2 + 2ab \Leftrightarrow a^2 + b^2 – 2ab \geq 0 \Leftrightarrow (a-b)^2 \geq 0\)
Αποδεικνύοντας την ανισότητα Cauchy-Schwarz
Θα προσπαθήσουμε να εφαρμόσουμε την ανισότητα Αριθμητικού – Γεωμετρικού μέσου για την απόδειξη.
Όπως σε όλες τις αποδείξεις ανισοτήτων με χρήση άλλων γνωστών ανισοτήτων η δύσκολη διεργασία είναι να βρεθεί πώς θα εφαρμοστεί αυτή. Γι’ αυτό το λόγο προσπαθούμε να συγκρίνουμε τις δύο ανισότητες για λίγους όρους αρχικά και έπειτα να κάνουμε γενική εφαρμογή.
Θέτουμε \(A = \sqrt{a_1 ^2 + a_2 ^2}, B = \sqrt{b_1 ^2 + b_2 ^2 }\) και έχουμε τη ζητούμενη να γράφεται διαδοχικά: \( (a_1 b_1 + a_2 b_2 )^2 \leq (a_1 ^2 + a_2 ^2) \cdot (b_1 ^2 + b_2 ^2 ) \Leftrightarrow (a_1 b_1 + a_2 b_2 ) \leq \sqrt{(a_1 ^2 + a_2 ^2)} \cdot \sqrt{(b_1 ^2 + b_2 ^2 )} \Leftrightarrow (a_1 b_1 + a_2 b_2 ) \leq A \cdot B \)
Όμως \(a_1 b_1 = \sqrt{a_1 ^2 \cdot b_1 ^2 }\)
και απο ανισότητα Αριθμητικού – Γεωμετρικού μέσου έχουμε: \(a_1 b_1 = \sqrt{a_1 ^2 \cdot b_1 ^2 } \leq \frac{a_1 ^2 + b_1 ^2}{2}\)
και \( a_2 b_2 = \sqrt{a_2 ^2 \cdot b_2 ^2 } \leq \frac{a_2 ^2 + b_2 ^2}{2}\)
οπότε: \( \frac{a_1 b_1 + a_2 b_2}{A \cdot B} \leq \frac{1}{2} \left( \frac{a_1 ^2 }{A^2} + \frac{b_1 ^2 }{B^2}\right) +\frac{1}{2} \left( \frac{a_2 ^2 }{A^2} + \frac{b_2 ^2 }{B^2}\right) = \frac{1}{2} \left( \frac{a_1 ^2 + a_2 ^2}{A^2} + \frac{b_1 ^2 + b_2 ^2}{B^2} \right) = \frac{1}{2}(1+1) = 1 \Leftrightarrow \)
δηλαδή: \( \frac{a_1 b_1 + a_2 b_2}{A\cdot B} \leq 1 \Leftrightarrow a_1 b_1 + a_2 b_2 \leq A\cdot B = \sqrt{a_1 ^2 + a_2 ^2}\sqrt{b_1 ^2 + b_2 ^2}\)
Η οποία είναι η ζητούμενη.
Η απόδειξη για n όρους μπορεί να γίνει εύκολα με μία τροποποίηση, θέτοντας \(A = \sqrt{a_1 ^2 + a_2 ^2 + \cdots a_n ^2},\ B = \sqrt{b_1 ^2 + b_2 ^2 + \cdots + b_n ^2}\)
Αναφορές
*Lohwater, Arthur (1982), ”Introduction to Inequalities”, Online e-book in PDF fomat.
*Wu H.H., Wu S., Various proofs of the Cauchy-Schwarz inequality, [εδώ].
Απολογισμός και υλικό ομίλου Μαθηματικών 2020-21
Τοπική και περιφερειακή δημοκρατία στην ΕΕ – 1999
Πηγή: RL-DEMOCRACY-EL.pdf
Φιλοσοφικές συμβολές…
Ανισότητα Andreescu
![\[\frac{ a_1^2 } { b_1 } + \frac{ a_2 ^2 } { b_2 } + \cdots + \frac{ a_n ^2 } { b_n } \geq \frac{ (a_1 + a_2 + \cdots+ a_n ) ^2 } { b_1 + b_2 + \cdots+ b_n }.\]](https://latex.artofproblemsolving.com/2/6/4/264fff665becc96f5f9e05a178f2a31ee3f2603f.png)
Είναι γνωστή και ως: T2 lemma, Engel’s form, or Sedrakyan’s inequality.
Αναφέρεται και ως Bergstrom’s Inequality με μία απόδειξη:
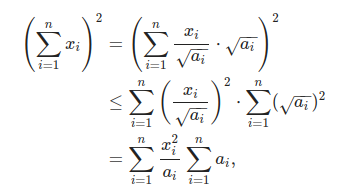
η οποία είναι ισοδύναμη με τη ζητούμενη.