Πηγή: MergedFile
Συντάκτης: shasapis
Θεωρητικές επισημάνσεις, ισχυρισμοί και αντιπαραδείγματα για την κατανόηση της θεωρίας περί του ορίου συναρτήσεων Στο σημε
Πηγή: ΣΗΜΕΙΩΜΑ 2 [06
(146) Σύνθεση συναρτήσεων => Ισότητα συναρτήσεων – mathematica.gr
Έστω οι συναρτήσεις $$f, g, h$$ με κοινό πεδίο ορισμού το $$\mathbb{R}$$.
Αν ισχύει $$g\circ f =h\circ f$$ και επιπλέον η $$f$$ έχει για σύνολο τιμών το $$\mathbb{R}$$ να αποδείξετε ότι:
$$g=h$$.
Παίρνουμε τυχόν $$x$$ για το οποίο υπάρχει $$y$$ με $$f(y)=x$$ και τότε $$g(x)=g(f(y))=h(f(y))=h(x)$$.
Να επισημάνω εδώ, κάτι που συχνά μπερδεύει και ξεχνιέται από τους μαθητές μας γιατί είναι ιδιαίτερα σημαντικό να δίνεται ότι το σύνολο τιμών της $$f: f(D_f ) = \mathbb{R}$$, διότι μέσω αυτού οι δύο συναρτήσεις $$h,g$$ λαμβάνουν όλες τις τιμές του πεδίου ορισμού τους που ειναι το $$\mathbb{R}$$ και έτσι εξασφαλίζεται η ισότητά τους.
Πηγή: (146) Σύνθεση συναρτήσεων => Ισότητα συναρτήσεων – mathematica.gr
wacom one pen tablet doesn’t work in ubuntu 16.04 version drivers – My WACOM One device is not working – Ask Ubuntu | Επιλογές Ubuntu – Ubuntu Applications
Πρακτικά: Διήμερο Διαλόγου για τη Διδασκαλία των Μαθηματικών
Openeclass Μαθηματικά σύμβολα
Πηγή: Τεχνολογικά- Προγραμματιστικά Νέα Τώρα – Tech News Now Gr
To toggle to the math mode, you must use the <m>…</m> tag. Apart from this tag, any html code can be used.
The math commands must be separated by a space character or surrounded by {}.
Examples :
- <m>S(f)(t)=a_{0}+sum{n=1}{+infty}{a_{n} cos(n omega t)+b_{n} sin(n omega t)}</m>
- <m>delim{lbrace}{matrix{3}{1}{{3x-5y+z=0} {sqrt{2}x-7y+8z=0} {x-8y+9z=0}}}{ }</m>
- <m>delim{|}{{1/N} sum{n=1}{N}{gamma(u_n)} – 1/{2 pi} int{0}{2 pi}{gamma(t) dt}}{|} <= epsilon/3</m>
Usual commands
x+y : 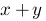
x-y : 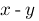
x*y : 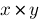
x/y : 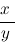
x^y : 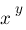
x_y : 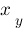
x<>y : 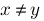
x>y : 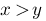
x>=y : 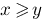
x<y : 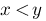
x<=y : 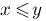
Parenthesis
visible : (x)
invisible : {x}
Math space
a~b : 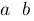
Greek letters
alpha : 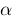
beta : 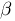
gamma : 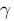
delta : 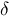
epsilon : 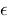
varepsilon : 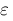
zeta : 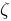
eta : 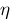
theta : 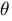
vartheta : 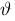
iota : 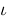
kappa : 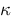
lambda : 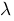
mu : 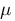
nu : 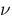
xi : 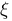
pi : 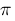
varpi : 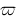
rho : 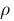
varrho : 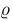
sigma : 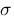
varsigma : 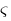
tau : 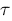
upsilon : 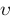
phi : 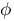
varphi : 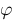
chi : 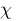
psi : 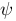
omega : 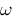
Gamma : 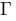
Lambda : 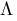
Sigma : 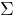
Psi : 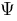
Delta : 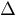
Xi : 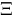
Upsilon : 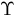
Omega : 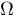
Theta : 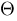
Pi : 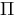
Phi : 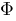
Symbols
infty : 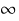
in : 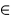
notin : 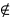
forall : 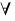
exists : 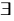
notexists : 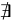
partial : 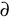
approx : 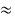
pm : 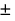
inter : 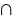
union : 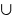
ortho : 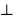
parallel : 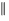
backslash : 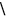
prime : 
wedge : 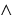
vert : 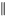
lbrace : {
rbrace : }
circ : 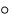
varnothing : 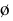
subset : 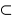
notsubset : 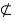
cdots : 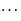
vdots : 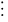
ddots : 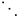
Arrows :
left : 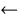
right : 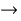
leftright : 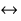
doubleleft : 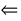
doubleright : 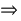
doubleleftright : 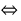
nearrow : 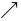
searrow : 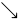
Sets
bbR : 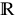
bbN : 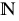
bbZ : 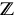
bbC : 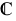
Roots
sqrt{a} : 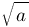
root{n}{a} : 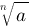
Limits
lim{a}{x} : 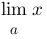
Big operators
int{a}{b}{x} : 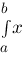
doubleint{a}{b}{x} : 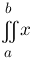
tripleint{a}{b}{x} : 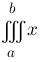
oint{a}{b}{x} : 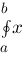
sum{a}{b}{x} : 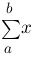
prod{a}{b}{x} : 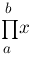
bigcup{a}{b}{x} : 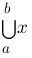
bigcap{a}{b}{x} : 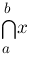
Delimiters
delim{[}{x}{]} : ![delim{[}{x}{]} delim{[}{x}{]}](https://presswiki.allmath.gr/wpwiki18/wp-content/uploads/2020/04/6b5c2ab858733a005ad3f8c858d2c0be.png)
delim{]}{x}{]} : ![delim{]}{x}{]} delim{]}{x}{]}](https://presswiki.allmath.gr/wpwiki18/wp-content/uploads/2020/04/5e8c71a1e42362bf2be0f8111e4c3159.png)
delim{[}{x}{[} : 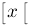
delim{]}{x}{[} : ![delim{]}{x}{[} delim{]}{x}{[}](https://presswiki.allmath.gr/wpwiki18/wp-content/uploads/2020/04/94b92579d53c853910546b82539bd013.png)
delim{lbrace}{x}{rbrace} : 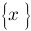
delim{|}{x}{|} : 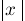
delim{vert}{x}{vert} : 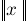
Matrix
matrix{num of lines}{num of columns}{first_element … last_element}
Example :
matrix{2}{3}{a b c d e f g} : 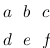
Tabular
tabular{lines description}{columns description}{first_element … last_element}
lines description : sequence of 1 (draw the horizontal line) or 0 (don’t draw the horizontal line) – the length of the sequence=num of lines+1
columns description : sequence of 1 (draw the vertical line) or 0 (don’t draw the vertical line) – the length of the sequence=num of columns+1
Examples :
tabular{111}{1111}{a b c d e f g} : 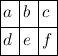
tabular{1001}{101}{1 2 3 4 5 6} : 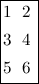
Constructions
vec{express} : 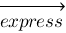
{express}under{foo} : 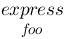
{express}over{foo} : 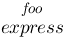
overline{express} : 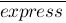
underline{express} : 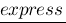
hat{express} : 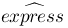
Πολλαπλή γραμμική παλινδρόμηση
Πηγή: 03_chapter02.pdf
Διερεύνηση των Προσδιοριστικών Παραγόντων και Μεθόδων Πρόβλεψης της Ζήτησης Ηλεκτρικής Ενέργειας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ
Διερεύνηση των Προσδιοριστικών Παραγόντων και Μεθόδων Πρόβλεψης της Ζήτησης Ηλεκτρικής Ενέργειας
ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Θεοχαρόπουλος Γεώργιος Επιβλέπων : Ιωάννης Ψαρράς Καθηγητής Ε.Μ.Π. Αθήνα, Ιούλιος 2015
Πηγή: DT2015-0218.pdf
16 μήνες Mathematica – Μαυρογιάννης 2010
Εξαιρετικά ζητήματα και σημειώσεις από συζητήσεις στη γνωστή ιστοσελίδα από το συνάδελφο Ν.Μαυρογιάννη.
Πηγή: Ó÷Ýäéï 1