Κατηγορία: Δραστηριότητες Α΄λυκείου

Μπορείτε να βρείτε κύκλο ο οποίος να διέρχεται από τρία σημεία στο επίπεδο; Υπάρχουν προϋποθέσεις;

Μπορείτε να βρείτε κύκλο ο οποίος να διέρχεται από τέσσερα σημεία στο επίπεδο; Υπάρχουν προϋποθέσεις;

Η παρουσίαση:

Δείτε το φύλλο εργασίας εδώ.

Δείτε την τάξη εργασίας geogebraclassroom εδώ.

Δείτε τη διαδραστική ταινία για τα εγγράψιμμα τετράπλευρα εδώ:

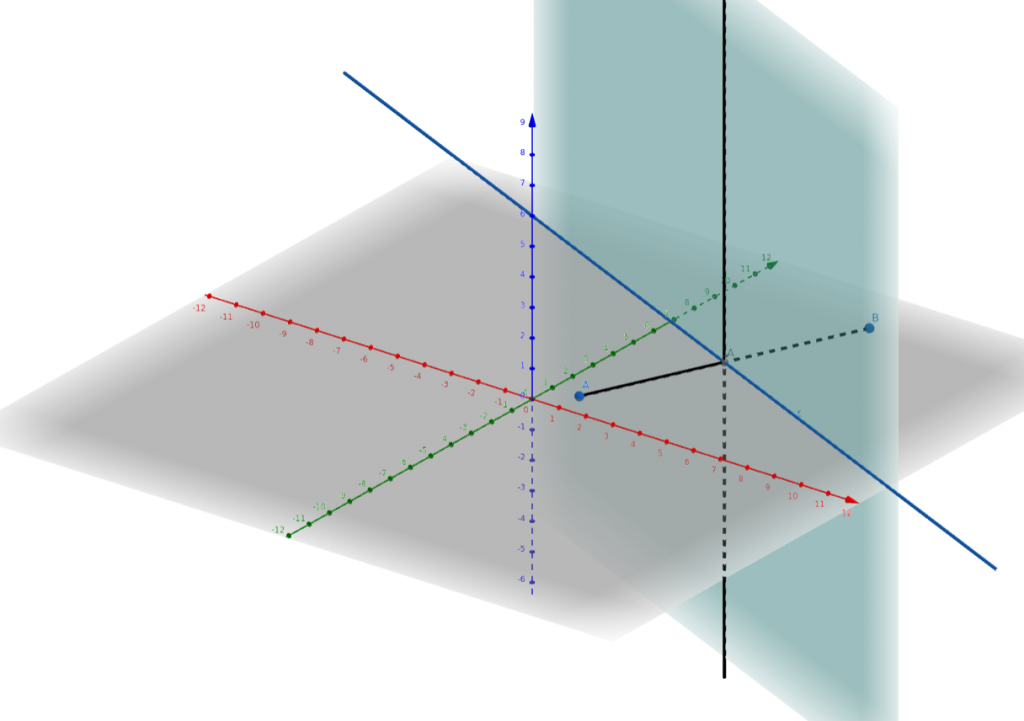
Στο σχήμα εδώ https://www.geogebra.org/3d/uecxjfeb  βλέπετε ένα ευθύγραμμο τμήμα που βρίσκεται στο γκρι επίπεδο.

Η μπλε ευθεία γραμμή είναι η μεσοκάθκετός του (ως γεωμετρικός τόπος σημείων του επιπέδου που ισαπέχουν από τα άκρα του ΑΒ).

Η μαύρη ευθεία γραμμή είναι η μεσοκάθετός του σε ένα άλλο επίπεδο που περιέχει το ΑΒ.

Αν φτιάξουμε «όλα» τα επίπεδα που περιέχουν το ΑΒ ( σκεφτείτε σε ένα τετράδιο ότι το ευθύγραμμο τμήμα της ράχης του περιέχεται σε όλα τα φύλλα του τετραδίου, καθένα από τα οποία είναι και ένα διαφορετικό επίπεδο) και τις μεσοκαθέτους του ΑΒ σε καθένα από αυτά, τότε

θα σχηματιστεί ένα επίπεδο κάθετο σε όλα αυτά τα επίπεδα, τα σημεία του οποίου επιπέδου θα έχουν την ιδιότητα να ισαπέχουνα από τα ΑΒ.

ΧΡησιμοποιείστε το εργαλείο μετακίνηση για να περιστρέψετε το σχήμα και να δείτε διαφορετικές οπτικές του.

https://www.geogebra.org/3d/uecxjfeb?embed