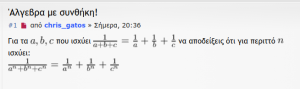Συντάκτης: shasapis
Η άνωση του Αρχιμήδη
Πρόγραμμα Μαθημάτων Προτύπου ΓΕΛ Ευαγγελικής Σχολής Σμύρνης 11-15/05/2020
ΠΡΟΓΡΑΜΜΑ/Κατανομή μαθητών 11/5 – 15/5/2020.
*ΠΡΟΣΟΧΗ! Θα προσέρχονται για υπογραφή της αίτησης-δήλωσης για τις Πανελλαδικές εξετάσεις οι μαθητές των τμημάτων που είναι στο σχολείο κάθε μέρα και έως την Πέμπτη 14/05/2020. Αν κάποιος δεν προσέλθει η δήλωσή του θα θεωρηθεί ως ΜΗ ΥΠΟΒΛΕΙΘΗΣΑ ! Οι μαθητές θα πρέπει να φέρουν και 3 φωτογραφίες οι τελειόφοιτοι, 1 φωτογραφία οι απόφοιτοι, καθώς επίσης και τις ταυτότητές τους.Για οποιαδήποτε διευκρίνηση να επικοινωνείτε με το σχολείο.
*Από Δευτέρα 11/5/2020 ξεκινούν τα, δια ζώσης, μαθήματα για την Γ΄λυκείου, σύμφωνα με το συνημμένο πρόγραμμα.
* Οι μαθητές Α΄και Β΄λυκείου θα παρακολουθήσουν πρόγραμμα τηλεκπαίδευσης όπως και την προηγούμενη εβδομάδα, ΣΥΜΦΩΝΑ ΜΕ ΤΟΝ ΣΥΝΗΜΜΕΝΟ ΠΡΟΓΡΑΜΜΑ. Δεν θα έρθουν σχολείο αυτήν την εβδομάδα.
* Για την ασφάλεια των μαθητών και των καθηγητών θα τηρηθούν αυστηρά όλες οι οδηγίες του Υπουργείου Υγείας και του Υπουργείου Παιδείας, γι αυτό και τη Δευτέρα-Τετάρτη-Παρασκευή θα προσέλθουν στο Σχολείο τα τμήματα ΓΘ1α, ΓΘ2α, ΓΥΓ1, ΓΑΣ.
* Την Τρίτη-Πέμπτη θα προσέλθουν στο Σχολείο τα τμήματα ΓΘ1β, ΓΘ2β, ΓΥΓ2, ΓΟΠ.
* Τα μαθήματα επιλογής Αγγλικά και Σχέδιο θα τα παρακολουθούν μόνο τα παιδιά που εξετάζονται τα αντίστοιχα μαθήματα Πανελλήνια.
* Η κατανομή των μαθητών στα τμήματα που χωρίζονται φαίνεται στις συνημμένες φωτογραφίες.
*Καθ’ όλη τη διάρκεια της εβδομάδας το σχολείο είναι κλειστό για οποιονδήποτε εκτός των μαθητών και των καθηγητών! Οποιοσδήποτε άλλος πρέπει να επικοινωνεί πρώτα με τη διεύθυνση για τη διευθέτηση όποιου ζητήματος.
Ευχαριστούμε.
Άλγεβρα με συνθήκη
Φύλλα Αριθμητικής για παιδιά
Πηγή: (675) Pinterest
Math is Fun
Πηγή: Math is Fun