Κατεβάστε από εδώ.




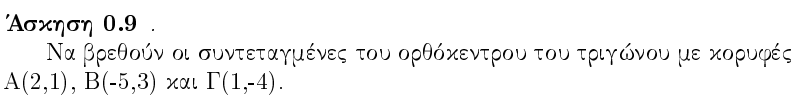

Wordpress Συλλέκτης: Γρήγορη αρχειοθέτηση-δημοσίευση αντικειμένων και προσωπικών δημιουργιών από www.arithmoi.gr. Δίνει χρήσιμο υλικό διδασκαλίας εδώ: https://ylikodidaskalias.wordpress.com/ ΟΛΟ ΤΟ ΥΛΙΚΟ εδώ και σύνδεσμοι μόνο προς αυτό.
Κατεβάστε από εδώ ολόκληρο το αρχείο.

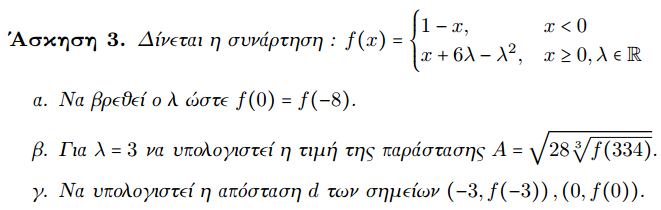
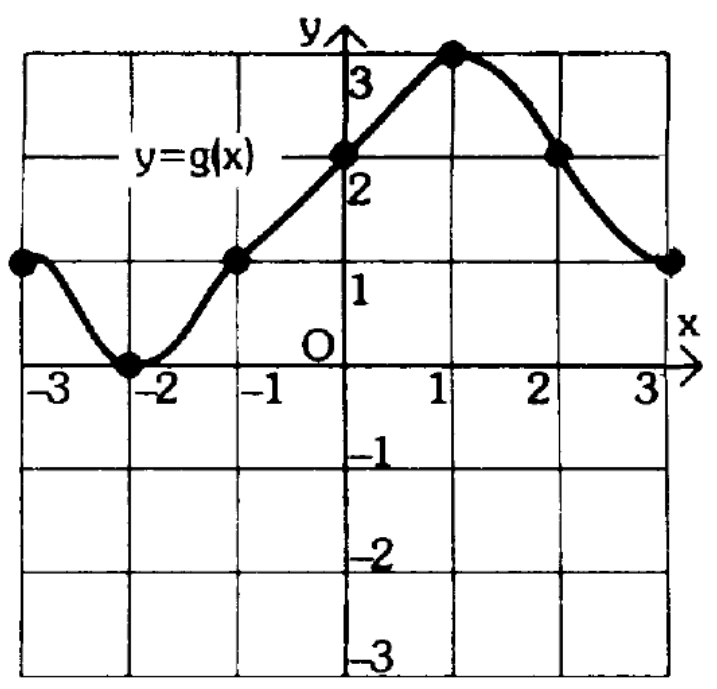
Άσκηση 4. Έστω η γραφική παράσταση της συνάρτησης y=g(x), όπως στο επόμενο σχήμα. Να απαντήσετε στα ερωτήματα: 




![]()






Μία πολύ καλή συλλογή, προσεγμένη με έγκυρες ασκήσεις (όχι αρλούμπες και σκουπίδια!)
http://users.sch.gr/mipapagr/images/aalg_sxol_2017-2018_papagrigorakis.pdf
Περισσότερες συλλογές ασκήσεων του συναδέλφου: εδώ.
Κατεβάστε όλα τα θέματα και τις λύσεις από εδώ.
Θέματα μικρών
Πρόβλημα 1.
 , τέτοιος ώστε οι αριθμοί
, τέτοιος ώστε οι αριθμοί  και
και 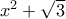 να είναι και οι δύο ρητοί.
να είναι και οι δύο ρητοί. , τέτοιος ώστε οι αριθμοί
, τέτοιος ώστε οι αριθμοί  και
και  να είναι και οι δύο ρητοί.
να είναι και οι δύο ρητοί.Πρόβλημα 2.
Θεωρούμε τετράγωνο  πλευράς
πλευράς  , το οποίο υποδιαιρούμε με ευθείες παράλληλες προς τις πλευρές του σε
, το οποίο υποδιαιρούμε με ευθείες παράλληλες προς τις πλευρές του σε  μικρά τετράγωνα πλευράς
μικρά τετράγωνα πλευράς 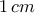 . Χρωματίζουμε
. Χρωματίζουμε  μικρά τετράγωνα μαύρα, ενώ όλα τα υπόλοιπα
μικρά τετράγωνα μαύρα, ενώ όλα τα υπόλοιπα  τετράγωνα είναι λευκά. Υποθέτουμε ότι υπάρχει θετικός ακέραιος
τετράγωνα είναι λευκά. Υποθέτουμε ότι υπάρχει θετικός ακέραιος  , τέτοιος ώστε, ανεξάρτητα από την θέση των
, τέτοιος ώστε, ανεξάρτητα από την θέση των  μαύρων μικρών τετραγώνων, υπάρχει ορθογώνιο εμβαδού
μαύρων μικρών τετραγώνων, υπάρχει ορθογώνιο εμβαδού 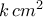 με πλευρές παράλληλες στις πλευρές του
με πλευρές παράλληλες στις πλευρές του  και με όλα τα μικρά τετράγωνα από τα οποία αποτελείται να είναι λευκά, που μπορεί να αποκοπεί από το τετράγωνο
και με όλα τα μικρά τετράγωνα από τα οποία αποτελείται να είναι λευκά, που μπορεί να αποκοπεί από το τετράγωνο  . Να βρεθεί η μέγιστη δυνατή τιμή του
. Να βρεθεί η μέγιστη δυνατή τιμή του  .
.
Πρόβλημα 3.
Θεωρούμε τους θετικούς ακεραίους  έτσι ώστε ο αριθμός
έτσι ώστε ο αριθμός  , όπου
, όπου  να είναι ακέραιος. Να αποδείξετε ότι, αν ο
να είναι ακέραιος. Να αποδείξετε ότι, αν ο  είναι περιττός, τότε ο
είναι περιττός, τότε ο  είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο.
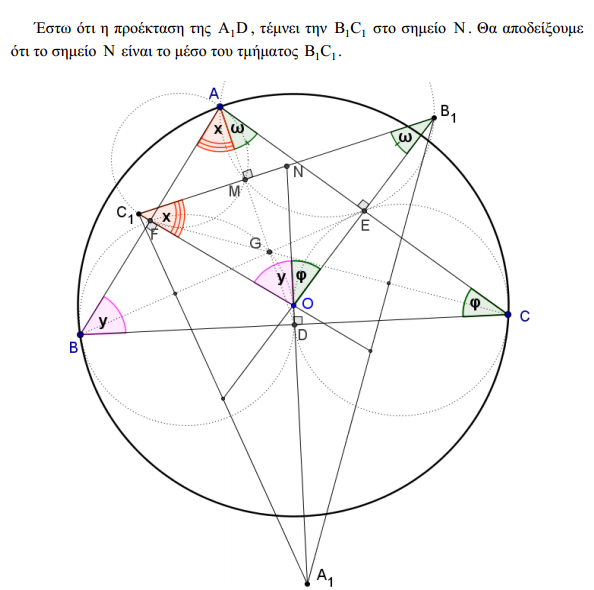
Πρόβλημα 4.
Δίνεται τρίγωνο 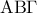 με
με  , εγγεγραμμένο σε κύκλο
, εγγεγραμμένο σε κύκλο  με κέντρο
με κέντρο  και ακτίνα
και ακτίνα  . Ονομάζουμε
. Ονομάζουμε  το αντιδιαμετρικό σημείο της κορυφής
το αντιδιαμετρικό σημείο της κορυφής  . Θεωρούμε επίσης τον κύκλο
. Θεωρούμε επίσης τον κύκλο 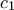 , του οποίου το κέντρο
, του οποίου το κέντρο  βρίσκεται επάνω στο τμήμα
βρίσκεται επάνω στο τμήμα  και περνάει από τα σημεία
και περνάει από τα σημεία 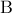 και
και  . Αν ο κύκλος
. Αν ο κύκλος 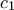 τέμνει την
τέμνει την  στο σημείο
στο σημείο 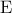 , να αποδείξετε ότι ο περιγεγραμμένος κύκλος του τριγώνου
, να αποδείξετε ότι ο περιγεγραμμένος κύκλος του τριγώνου  , έστω
, έστω  , εφάπτεται του περιγεγραμμένου κύκλου
, εφάπτεται του περιγεγραμμένου κύκλου  του τριγώνου
του τριγώνου 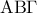 .
.
——————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————–
Θέματα μεγάλων
Πρόβλημα 1.
Θεωρούμε την ακολουθία  που ορίζεται αναδρομικά από την σχέση
που ορίζεται αναδρομικά από την σχέση  με
με  , όπου
, όπου  είναι θετικοί ακέραιοι και ο
είναι θετικοί ακέραιοι και ο  δεν διαιρεί τον ακέραιο
δεν διαιρεί τον ακέραιο  . Αν για κάποιο θετικό ακέραιο
. Αν για κάποιο θετικό ακέραιο  ο
ο 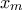 είναι τέλειο τετράγωνο ρητού αριθμού, να αποδείξετε ότι και ο
είναι τέλειο τετράγωνο ρητού αριθμού, να αποδείξετε ότι και ο  είναι τέλειο τετράγωνο ρητού αριθμού.
είναι τέλειο τετράγωνο ρητού αριθμού.
Πρόβλημα 2.
Δίνονται οξυγώνιο τρίγωνο 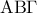 με
με  και ο περιγεγραμμένος κύκλος του
και ο περιγεγραμμένος κύκλος του  με κέντρο
με κέντρο  και ακτίνα
και ακτίνα  . Στα μικρά τόξα
. Στα μικρά τόξα  και
και 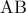 θεωρούμε τα σημεία
θεωρούμε τα σημεία  και
και 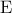 αντίστοιχα. Έστω
αντίστοιχα. Έστω  είναι το σημείο τομής των
είναι το σημείο τομής των  και
και  είναι το δεύτερο κοινό σημείο των περιγεγραμμένων κύκλων των τριγώνων
είναι το δεύτερο κοινό σημείο των περιγεγραμμένων κύκλων των τριγώνων  , έστω
, έστω 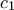 , και
, και 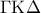 , έστω
, έστω  . Να αποδείξετε ότι : τα σημεία
. Να αποδείξετε ότι : τα σημεία  ,
, 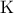 ,
,  είναι συνευθειακά, αν και μόνο αν, το σημείο
είναι συνευθειακά, αν και μόνο αν, το σημείο 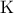 ανήκει στην συμμετροδιάμεσο του τριγώνου
ανήκει στην συμμετροδιάμεσο του τριγώνου 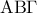 , που αντιστοιχεί στην κορυφή
, που αντιστοιχεί στην κορυφή  .
.
Σημείωση: Συμμετροδιάμεσος τριγώνου είναι η συμμετρική ευθεία της διαμέσου, ως προς την διχοτόμο, που περνάει από την ίδια κορυφή με την διάμεσο.
Πρόβλημα 3.
 με
με 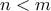 και διακεκριμένοι πραγματικοί αριθμοί
και διακεκριμένοι πραγματικοί αριθμοί  . Να βρεθούν όλα τα πολυώνυμα
. Να βρεθούν όλα τα πολυώνυμα  με πραγματικούς συντελεστές, βαθμού το πολύ
με πραγματικούς συντελεστές, βαθμού το πολύ  , για τα οποία ισχύει η ισότητα
, για τα οποία ισχύει η ισότητα 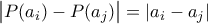 για κάθε
για κάθε 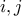 με
με  .
.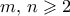 με
με 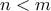 . Να εξετάσετε αν υπάρχει πολυώνυμο
. Να εξετάσετε αν υπάρχει πολυώνυμο  με πραγματικούς συντελεστές, βαθμού
με πραγματικούς συντελεστές, βαθμού  καθώς και διακεκριμένοι πραγματικοί αριθμοί
καθώς και διακεκριμένοι πραγματικοί αριθμοί  , τέτοιοι ώστε
, τέτοιοι ώστε  για κάθε
για κάθε 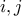 με
με  .
.Πρόβλημα 4.
Θεωρούμε  σημεία στο επίπεδο,
σημεία στο επίπεδο,  , ανά τρία μη-συνευθειακά. Ονομάζουμε
, ανά τρία μη-συνευθειακά. Ονομάζουμε  το πλήθος των παραλληλογράμμων εμβαδού
το πλήθος των παραλληλογράμμων εμβαδού  που σχηματίζονται με κορυφές αυτά τα σημεία. Να αποδείξετε ότι
που σχηματίζονται με κορυφές αυτά τα σημεία. Να αποδείξετε ότι  για κάθε
για κάθε  .
.