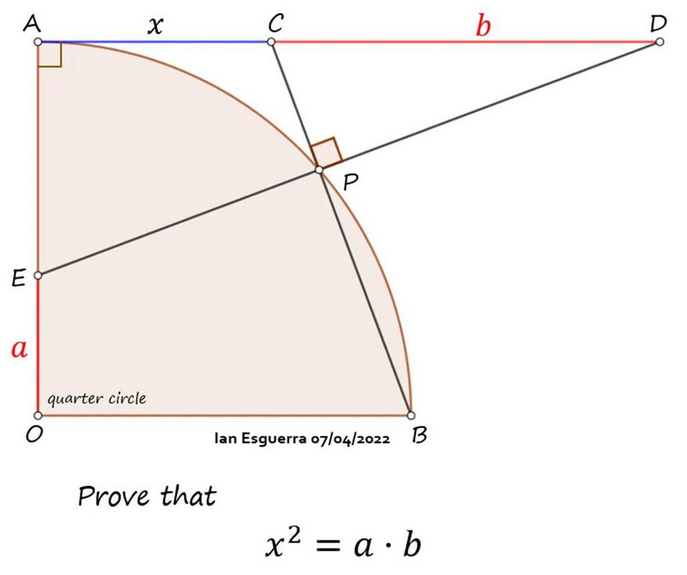
https://www.facebook.com/IanEsguerra0/photos/a.106679811952642/124019676885322/
Wordpress Συλλέκτης: Γρήγορη αρχειοθέτηση-δημοσίευση αντικειμένων και προσωπικών δημιουργιών από www.arithmoi.gr. Δίνει χρήσιμο υλικό διδασκαλίας εδώ: https://ylikodidaskalias.wordpress.com/ ΟΛΟ ΤΟ ΥΛΙΚΟ εδώ και σύνδεσμοι μόνο προς αυτό.
τα περισσότερα από αυτά είναι σε προχωρημένο επίπεδο. Για όσους τώρα ξεκινούν μπορούν για αρχή να κοιτάξουν την υπάρχουσα Ελληνική βιβλιογραφία. International Mathematical Olympiad D. Djukic, V. Jankovic, I. Matic, N. Petrovic : The IMO Compendium 1959-2009, Springer, 2011. M. Becheanu : International Mathematical Olympiads 1959-2000. Problems. Solutions. Results, Academic Distribution Center, Freeland, USA, 2001.
I. Reiman, J. Pataki, A. Stipsitz : International Mathematical Olympiad: 1959–1999 , Anthem Press, London, 2002. I. Cuculescu : International Mathematical Olympiads for Students (in Romanian), Editura Tehnica, Bucharest, 1984. A.A. Fomin, G.M. Kuznetsova : International Mathematical Olympiads (in Russian), Drofa, Moscow, 1998. M. Aassila : 300 Defis Mathematiques (in French), Ellipses, Paris, 2001. M.S. Klamkin : International Mathematical Olympiads 1979–1986, MAA, Washington, D.C., 1988. S.L. Greitzer : International Mathematical Olympiads 1959-1977, MAA, Washington, D.C., 1978. V. Jankovic, V. Micic : IX and XIX International Mathematical Olympiads, MS of Serbia, Belgrade, 1997. M.S. Klamkin : International Mathematical Olympiads 1979–1985 and Forty Supplementary Problems , MAA, Washington, D.C., 1986. E.A. Morozova, I.S. Petrakov, V.A. Skvortsov : International Mathematical Olympiads (in Russian), Prosveshchenie, Moscow, 1976. M. Asic et al. : International Mathematical Olympiads (in Serbian) , MS of Serbia, Belgrade, 1986. V. Jankovic, Z. Kadelburg, P. Mladenovic : International and Balkan Mathematical Olympiads 1984–1995 (in Serbian), MS of Serbia, Belgrade, 1996. Other Mathematical Olympiads T. Andreescu, K. Kedlaya, P. Zeitz : Mathematical Olympiads 1995-1996, Problems and Solutions from Around the World, AMC, 1997. T. Andreescu, Z. Feng : Mathematical Olympiads 2000-2001, Problems and Solutions from Around the World, MAA, 2003. A. Gardiner : The Mathematical Olympiad Handbook, Oxford, 1997. A. Liu : Hungarian Problem Book III, MAA, 2001. A.M. Slinko : USSR Mathematical Olympiads 1989–1992, AMT, Canberra, 1997. A. Liu : Chinese Mathematical Competitions and Olympiads 1981-1993, AMT, Canberra, 1998. I. Tomescu et al. : Balkan Mathematical Olympiads 1984-1994 (in Romanian), GIL Publishing House, Zalau, 1996. K.S. Kedlaya, B. Poonen, R. Vakil : The William Lowell Putnam Mathematical Competition 1985-2000 Problems, Solutions and Commentary, MAA, 2002. D. Fomin, A. Kirichenko : Leningrad Mathematical Olympiads 1987-1991, MathPro Press, 1994. M.E. Kuczma : 144 Problems of the Austrian-Polish Mathematics Competition 1978–1993, The Academic Distribution Center, Freeland, Maryland, 1994. T. Andreescu, Z. Feng : Mathematical Olympiads 1999-2000, Problems and Solutions from Around the World, MAA, 2002. Lausch, Bosch Giral : Asian Pacific Mathematics Olympiads 1989–2000, AMT, Canberra, 1994. Kurshak, Hajos, Neukomm, Suranyi : Hungarian Problem Book II, MAA, 1967. Kurshak, Hajos, Neukomm, Suranyi : Hungarian Problem Book I, MAA, 1967. M.S. Klamkin : USA Mathematical Olympiads 1972–1986, MAA, Washington, D.C., 1988. T. Andreescu, K. Kedlaya : Mathematical Olympiads 1997-1998, Problems and Solutions from Around the World, AMC, 1999. T. Andreescu, Z. Feng : Mathematical Olympiads 1998-1999, Problems and Solutions from Around the World, MAA, 2000. Lausch, Taylor : Australian Mathematical Olympiads 1979–1995, AMT, Canberra, 1997. Peter J. Taylor : International Mathematics Tournament of the Towns, Book 1: 1980-1984, AMT Publishing, 1993. T. Andreescu, K. Kedlaya : Mathematical Olympiads 1996-1997, Problems and Solutions from Around the World, AMC, 1998. Peter J. Taylor : International Mathematics Tournament of the Towns, Book 3: 1989-1993, AMT Publishing, 1994. Andrei M. Storozhev : International Mathematics Tournament of the Towns, Book 5: 1997-2002, AMT Publishing, 2006. Peter J. Taylor : International Mathematics Tournament of the Towns, Book 2: 1984-1989, AMT Publishing, 2003. L. Hahn : New Mexico Mathematics Contest Problem Book, University of New Mexico Press, 2005. G.L. Alexanderson, L.F. Klosinski, L.C. Larson : The William Lowell Putnam Mathematical Competition, Problems and Solutions: 1965-1984, MAA, 1985. Peter J. Taylor, Andrei M. Storozhev : International Mathematics Tournament of the Towns, Book 4: 1993-1997, AMT Publishing, 1998. A.M. Gleason, R.E. Greenwood, L.M. Kelly : The William Lowell Putnam Mathematical Competition, Problems and Solutions: 1938-1964, MAA, 1980. Other Problem Solving Books P. Zeitz : The Art and Craft of Problem Solving, Wiley; International Student edition, 2006. T. Andreescu, D. Andrica : 360 Problems for Mathematical Contests, GIL Publishing House, Zalau, 2003. L. Moisotte : 1850 exercices de mathemathique , Bordas, Paris, 1978. A. Engel : Problem Solving Strategies, Springer-Verlag, 1999. C.R. Pranesachar, S.A. Shailesh, B.J. Venkatachala, C.S. Yogananda : Mathematical Challenges from Olympiads, Interline Publishing Pvt. Ltd., Bangalore, 1995. A.M. Yaglom, I.M. Yaglom : Challenging Mathematical Problems with Elementary Solutions, Dover Publications, 1987. M. Aigner, G.M. Ziegler : Proofs from THE BOOK, Springer-Verlag; 3rd edition, 2003. R. Gelca, T. Andreescu : Putnam and Beyond, Springer 2007. T. Andreescu, B. Enescu : Mathematical Olympiad Treasures, Birkhauser, Boston, 2003. Z. Stankova, T. Rike : A Decade of the Berkeley Math Circle , American Mathematical Society, 2008 E. Lozansky, C. Rousseau : Winning Solutions, Springer-Verlag, New York, 1996. R.L. Graham, D.E. Knuth, O. Patashnik : Concrete Mathematics, 2nd Edition, Addison-Wesley, 1989. T. Andreescu, R. Gelca : Mathematical Olympiad Challenges, Birkhauser, Boston, 2000. R. Vakil : A Mathematical Mosaic: Patterns and Problem Solving (2nd. ed.), M.A.A., 2007 G. Polya : How to Solve It: A New Aspect of Mathematical Method, Princeton University Press R. Honsberger : In Polya \?s Footsteps: Misscelaneous Problems and Essays, M.A.A., 1997 R. Honsberger : From Erdos to Kiev: Problems of Olympiad Caliber, M.A.A., 1996 E.J. Barbeau, M.S. Klamkin. W.O.J. Moser : Five Hundred Mathematical Challenges , MAA, 1995. T. Andreescu, G. Dospinescu : Problems from the Book, XYZ Press, 2008. L.C. Larson : Problem Solving Through Problems, Springer-Verlag, 1983. Algebra, Analysis, and Inequalities P.K. Hung: Secrets in Inequalities, GIL Publishing House, 2007 T. Andreescu, V. Cartoaje, G. Dospinescu, M. Lascu : Old and New Inequalities , GIL Publishing House, 2004. E.J. Barbeau : Polynomials , Springer-Verlag, 2003. N.D. Kazarinoff : Geometric Inequalities , MAA, 1975. C.G. Small : Functional Equations and How to Solve Them, Springer, 2006 A.S. Posamentier, C.T. Salkind : Challenging Problems in Algebra, Dover Books in Mathematics, 1996. T. Andreescu, D. Andrica : Complex Numbers from A to … Z, Birkhauser, Boston, 2005. P.S. Bullen, D.S. Mitrinovic , M. Vasic : Means and Their Inequalities, Springer-Verlag, 1989. M. Arsenovic, V. Dragovic : Functional Equations (in Serbian) , MS of Serbia, Belgrade, 1999. Z. Cvetkovski : Inequalities – Theorems, Techniques and Selected Problems , Springer, 2012. D.S. Mitrinovic, J.E. Pecaric, V. Volenec : Recent Advances in Geometric Inequalities, Kluwer Academic Publishers, 1989. J. Hardy, J.E. Littlewood, G. Polya : Inequalities, Cambridge University Press; 2nd edition, 1998. D.S. Mitrinovic , J. Pecaric, A.M Fink : Classical and New Inequalities in Analysis, Springer-Verlag, 1992. G.H. Herman, R. Kucera, K. Dilcher : Equations and Inequalities, Springer, 2000 Z. Kadelburg, D. Djukic, M. Lukic, I. Matic : Inequalities (in Serbian), MS of Serbia, Belgrade, 2003. Geometry and Trigonometry P.S. Modenov : Problems in Geometry, MIR, Moscow, 1981. H.S.M. Coxeter : Introduction to Geometry , John Willey and Sons, New York, 1969 T. Andreescu, Z. Feng : 103 Trigonometry Problems: From the Training of the USA IMO Team, Birkhauser Boston, 2004. I.M. Yaglom : Geometric Transformations, Vol. II, MAA, 1968. A.P. Kiselev (author), A. Givental (editor) : Kiselev\?s Geometry / Book I. Planimetry (Hardcover) , Sumizdat, 2006 P.S. Modenov, A.S. Parhomenko : Geometric Transformations, Academic Press, New York, 1965. I.M. Yaglom : Geometric Transformations, Vol. I, MAA, 1962 N. Altshiller-Court : College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle, Dover Publications, 2007 V.V. Prasolov, V.M. Tikhomirov : Geometry, American Mathematical Society, 2001. C.J. Bradley : Challenges in Geometry : for Mathematical Olympians Past and Present, Oxford University Press, 2005. L. Hahn : Complex Numbers and Geometry, New York, 1960. I.M. Yaglom : Geometric Transformations, Vol. III, MAA, 1973. A.S. Posamentier, C.T. Salkind : Challenging Problems in Geometry, Dover Publications, 1996. I.F. Sharygin : Problems in Plane Geometry, Imported Pubn, 1988. T. Andreescu, O. Mushkarov, L. Stoyanov : Geometric Problems on Maxima and Minima, Birkhauser Boston, 2005. H.S.M. Coxeter, S.L. Greitzer : Geometry Revisited , Random House, New York, 1967 Number Theory M.Th. Rassias : Problem-Solving and Selected Topics in Number Theory : In the Spirit of the Mathematical Olympiads Foreword by Preda Mihailescu, Springer, New York, 2011. I. Nagell : Introduction to Number Theory, John Wiley and Sons, Inc., New York, Stockholm, 1951. W. Sierpinski : 250 Problems in Elementary Number Theory, American Elsevier Publishing Company, Inc., New York, PWN, Warsaw, 1970. E.J. Barbeau : Pell?s Equation , Springer-Verlag, 2003. W. Sierpinski : Elementary Theory of Numbers, Polski Academic Nauk, Warsaw, 1964. A. Baker : A Concise Introduction to the Theory of Numbers , Cambridge University Press, Cambridge, 1984. I.M. Vinogradov : The Method of Trigonometrical Sums in the Theory of Numbers, Dover Books in Mathematics, 2004. I.M. Vinogradov : Elements of Number Theory, Dover Publications, 2003. T. Andreescu, D. Andrica : An Introduction to the Diophantine Equations, GIL Publishing House, Zalau, 2002. R.K. Guy : Unsolved Problems in Number Theory, Springer-Verlag, 3rd edition, 2004. L.J. Mordell : Diophantine Equations, Academic Press, London and New York, 1969. J. Tattersall : Elementary Number Theory in Nine Chapters (2nd. ed.), Cambridge University Press, 2005. I. Niven, H.S. Zuckerman, H.L. Montgomery : An Introduction to the Theory of Numbers , John Wiley and Sons, Inc., 1991. V. Micic, Z. Kadelburg, D. Djukic : Introduction to Number Theory (in Serbian), 4th edition, MS of Serbia, Belgrade, 2004. G.H. Hardy, E.M. Wright : An Introduction to the Theory of Numbers, Oxford University Press; 5th edition, 1980. T. Andreescu, D. Andrica, Z. Feng : 104 Number Theory Problems, Birkhauser, Boston 2006 Combinatorics, Graph Theory, and Game Theory T. Andreescu, Z. Feng : 102 Combinatorial Problems, Birkhauser Boston, 2002. S. Lando : Lectures on Generating Functions, A.M.S., 2003. I. Tomescu, R.A. Melter : Problems in Combinatorics and Graph Theory, John Wiley and Sons, 1985. C. Chuan-Chong, K. Khee-Meng : Principles and Techiques in Combinatorics, World Scientific Publishing Company, 1992. H.S. Wilf : Generatingfunctionology , Academic Press, Inc.; 3rd edition, 2006. R.Brualdi : Introductory Combinatorics (4th ed.), Prentice-Hall, 2004. E.L. Berlekamp, J.H. Conway, R.K. Guy : Winning Ways for Your Mathematical Plays (Vol. 1), AK Peters, Ltd., 2nd edition, 2001. D. Stevanovic, M. Milosevic, V. Baltic : Discrete Mathematics: Problem Book in Elementary Combinatorics and Graph Theory (in Serbian), MS of Serbia, Belgrade, 2004. T. Andreescu, Z. Feng : A Path to Combinatorics for Undergraduates: Counting Strategies, Birkhauser Boston, 2003. P. Mladenovic : Combinatorics (in Serbian), 3rd edition, MS of Serbia, Belgrade, 2001. R.P. Stanley : Enumerative Combinatorics, Volumes 1 and 2, Cambridge University Press; New Ed edition, 2001. E.L. Berlekamp, J.H. Conway, R.K. Guy : Winning Ways for Your Mathematical Plays (Vol. 4), AK Peters, Ltd., 2nd edition, 2004. E.L. Berlekamp, J.H. Conway, R.K. Guy : Winning Ways for Your Mathematical Plays (Vol. 3), AK Peters, Ltd., 2nd edition, 2003. J.H. van Lint, R.M. Wilson : A Course in Combinatorics, second edition, Cambridge University Press, 2001. E.L. Berlekamp, J.H. Conway, R.K. Guy : Winning Ways for Your Mathematical Plays (Vol. 2), AK Peters, Ltd., 2nd edition, 2003. Πηγή: imomath
Θεματογραφία Μαθηματικών Διαγωνισμών από όλον τον κόσμο.
Περισσότερα από 20000 θέματα.
Πηγές: http://www.artofproblemsolving.com/Forum/resources.php , http://mathandmultimedia.com/2011/03/14/mathematics-contest-problems/
και για τους Ελληνικούς Μαθηματικούς Διαγωνισμούς από την Ε.Μ.Ε. εδώ και γενικότερα για εξάσκηση στο www.mathematica.gr.
Ειδικότερα, θέματα για όλους – εισαγωγικά εδώ, γενικά ομαδοποιημένα θέματα για διαγωνισμούς και γενικότερα ακόμα ενδιαφέρουσες ασκήσεις για μαθητές και μόνο. Σε όλες αυτές τις κατηγορίες οι μαθητές μπορούν ανάλογα με το επίπεδό τους και το ενδιαφέρον τους να εξασκηθούν σε σημαντικά κομμάτια είτε της ύλης των διαγωνισμών, όπου εμφανίζονται ιδιαιτέρως ενδιαφέροντα προβλήματα, αλλά και θέματα εκτός μαθηματικών διαγωνισμών που εφάπτονται της ύλης του σχολείου και ενισχύουν την κοινωνική οπτική τους.
Η εγγραφή σε ένα φόρουμ σχετικού με μαθηματικά και η ενεργή συμμετοχή στη συζήτηση αποτελεί συμπληρωματική και ουσιαστικότατη ενέργεια στην επίλυση ενός προβλήματος, διότι διαφαίνονται τόσο οι σκέψεις, όσο και οι γενικότεροι προβληματισμοί του λύτη.
Κατά δυσκολία:BEGINNERS
INTERMEDIATE
OLYMPIAD LEVEL
Κατά είδος και Χώρα:
![\[\frac{ a_1^2 } { b_1 } + \frac{ a_2 ^2 } { b_2 } + \cdots + \frac{ a_n ^2 } { b_n } \geq \frac{ (a_1 + a_2 + \cdots+ a_n ) ^2 } { b_1 + b_2 + \cdots+ b_n }.\]](https://latex.artofproblemsolving.com/2/6/4/264fff665becc96f5f9e05a178f2a31ee3f2603f.png)
Είναι γνωστή και ως: T2 lemma, Engel’s form, or Sedrakyan’s inequality.
Αναφέρεται και ως Bergstrom’s Inequality με μία απόδειξη:
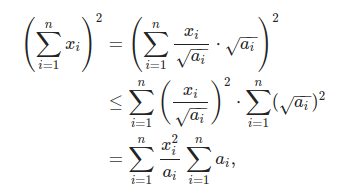
η οποία είναι ισοδύναμη με τη ζητούμενη.