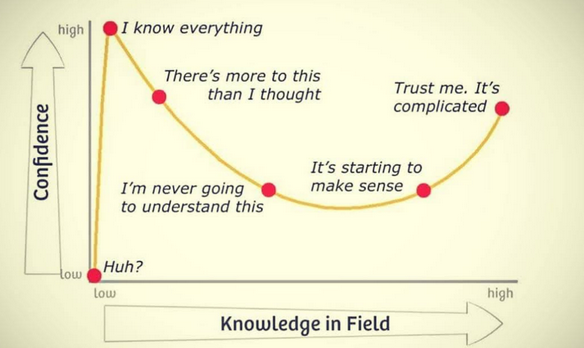
Γνώση και αυτοπεποίθηση:
Wordpress Συλλέκτης: Γρήγορη αρχειοθέτηση-δημοσίευση αντικειμένων και προσωπικών δημιουργιών από www.arithmoi.gr. Δίνει χρήσιμο υλικό διδασκαλίας εδώ: https://ylikodidaskalias.wordpress.com/ ΟΛΟ ΤΟ ΥΛΙΚΟ εδώ και σύνδεσμοι μόνο προς αυτό.
Μόνο όσα θέλω να είναι πλήρως ιδιωτικά
A hundred and twenty years ago, divers discovered a shipwreck off the island of Antikythera in Greece. What they found changed our understand of human history. The mysterious Antikythera Mechanism has captured the imagination of archaeologists, mathematicians, and scientists ever since. Now, using the latest 3D x-ray and modelling technology, experts are unravelling the secrets of what this machine may have been capable of. Video by Harriet Constable
Πηγή: Unlocking the secrets of the world’s oldest computer – BBC Reel