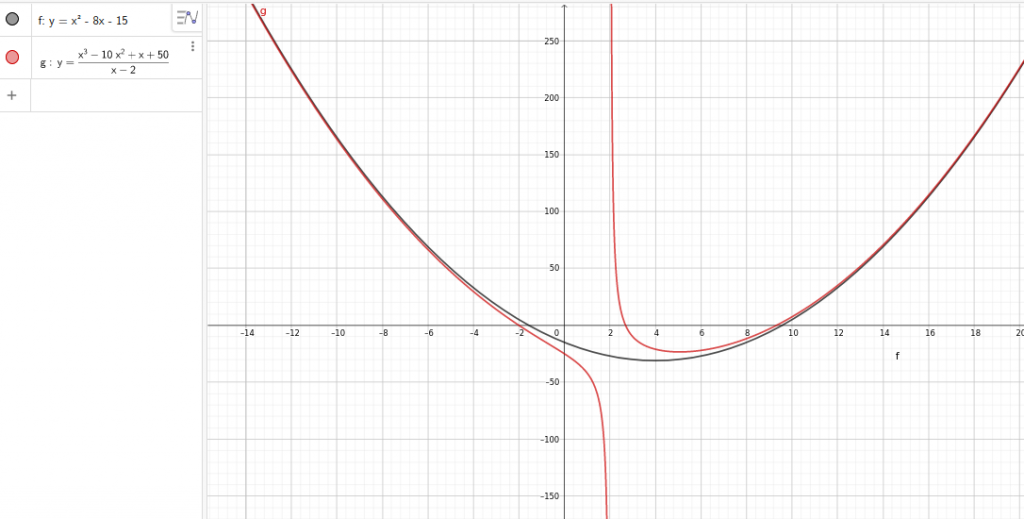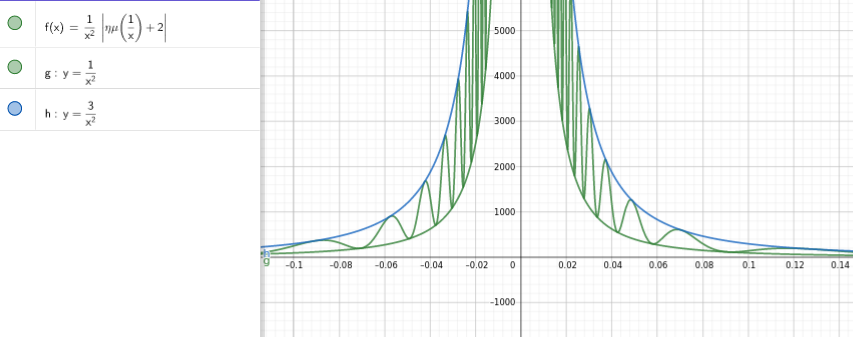
Αν γενικεύσουμε την έννοια της ασύμπτωτης για να συμπεριλάβει καμπύλες θα μπορούσαμε να γράψουμε ότι η
\( f(x) = \frac{1}{x^2 } \left| \sin(\frac{1}{x}) +2 \right| \)
έχει ασύμπτωτη στο \(+\infty\) την \(y=\frac{1}{x^2} \),
διότι \(\lim_{x\to +\infty} f(x) – y =0\)
αλλά είναι όμως μοναδική όπως η ευθεία;
https://www.geogebra.org/m/yxansf9j#material/sej93wrr