https://www.geogebra.org/m/tarqeb7d#material/mgm7qeuc
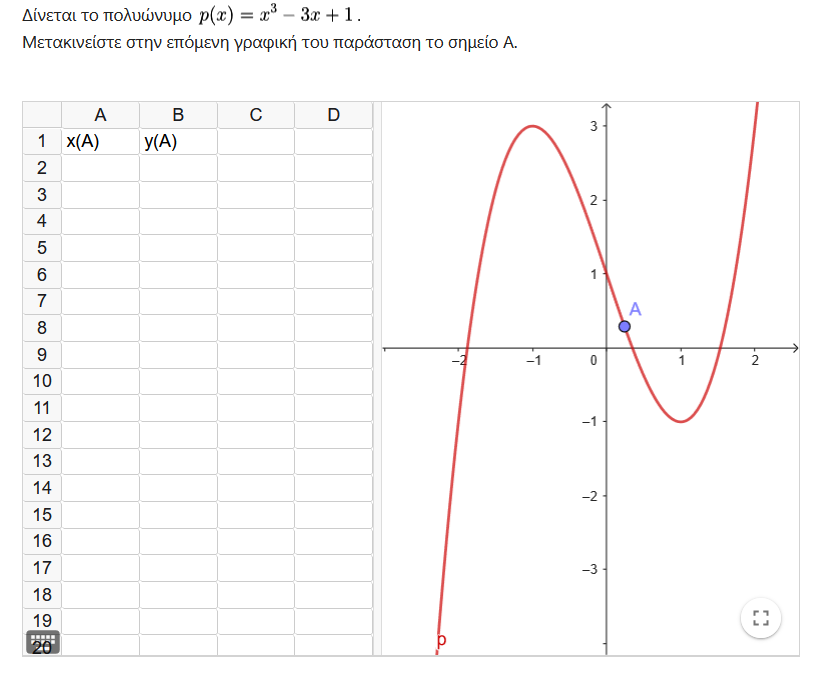
Wordpress Συλλέκτης: Γρήγορη αρχειοθέτηση-δημοσίευση αντικειμένων και προσωπικών δημιουργιών από www.arithmoi.gr. Δίνει χρήσιμο υλικό διδασκαλίας εδώ: https://ylikodidaskalias.wordpress.com/ ΟΛΟ ΤΟ ΥΛΙΚΟ εδώ και σύνδεσμοι μόνο προς αυτό.
Δείτε και εδώ: https://www.geogebra.org/calculator/pra4xees
Εμφανίστε σε πλήρη οθόνη το παρακάτω, μετακινώντας προς τα κάτω τα βασικά εργαλεία και εμφανίζοντας το

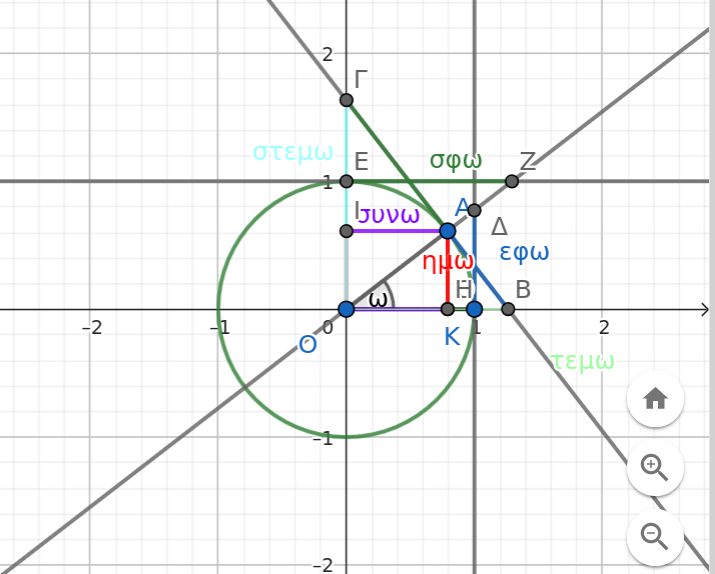
Σύντομη ιστορία τριγωνομετρίας:
Παραμετρικές ευθείες με σημείο τομής σε κύκλο.
https://www.geogebra.org/calculator/f66rqjvx
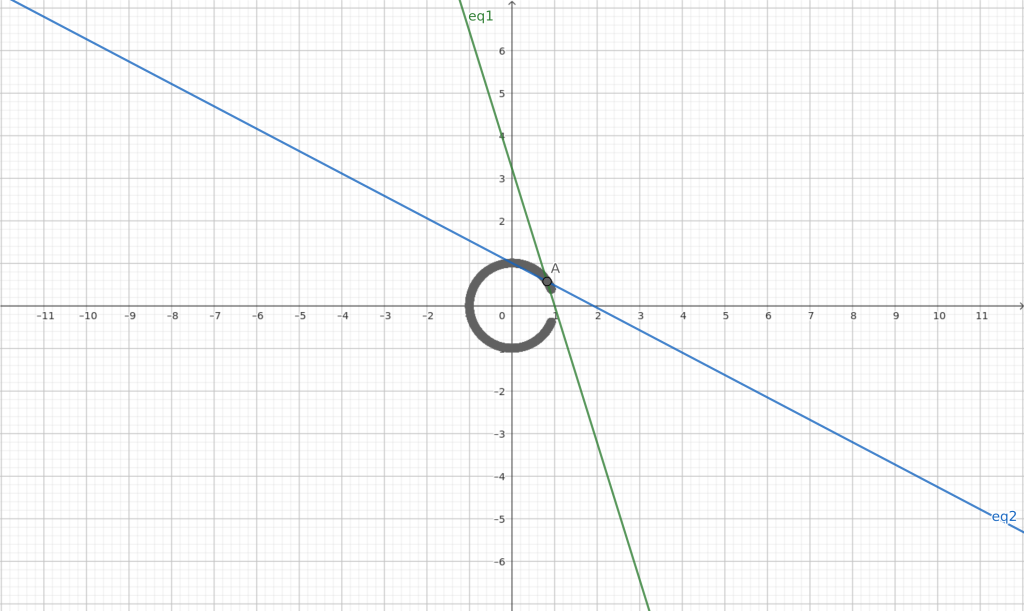
Αν \(m \in \mathbb{R} \) το σημείο τομής Α των δύο ευθειών καλύπτουν ολόκληρο τον κύκλο;