Κατηγορία: Γεωμετρία Α λυκείου
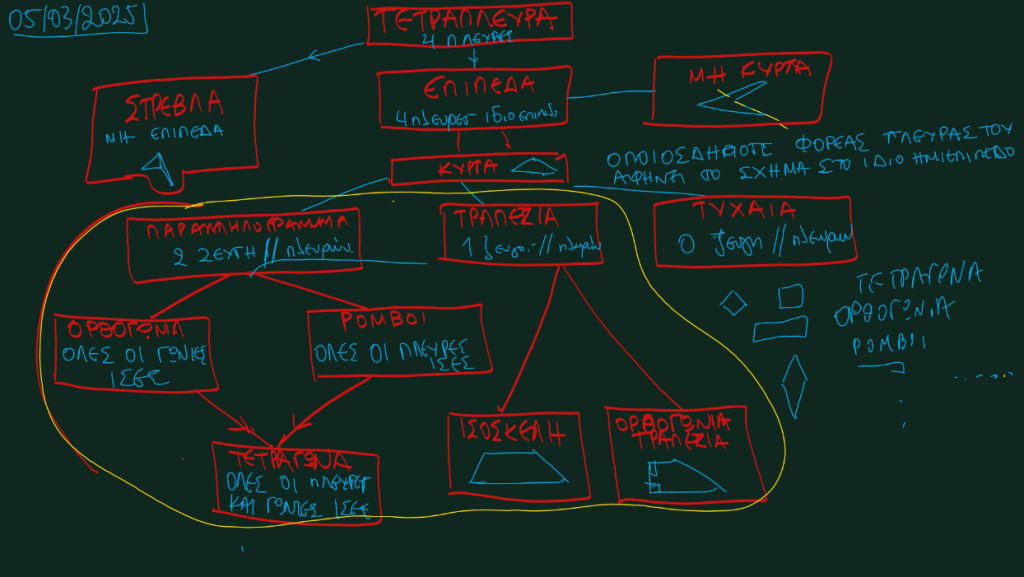
Ταξινόμηση Τετραπλεύρων
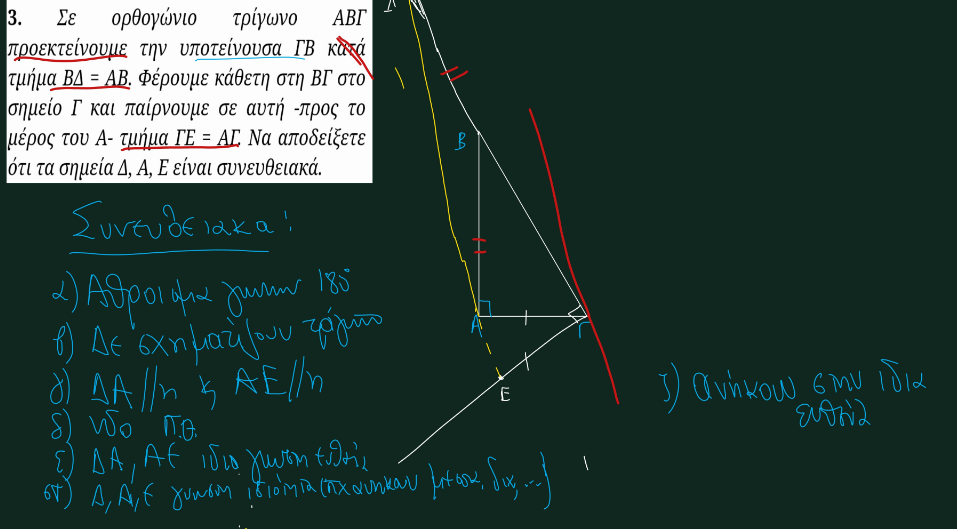
Συνευθειακά σημεία Πότε και πώς
Τετράπλευρο σε τετράπλευρο Διερευνητική εργασία
Τετράπλευρο σε τετράπλευρο Περιγραφή:
Δίνεται το τετράπλευρο ΑΒΓΔ, όπως στο σχήμα.
Αν Ε, Ζ, Η, Θ μέσα των αντιστοίχων πλευρών του, τότε:
α) Βρείτε όσες περισσότερες παρατηρήσεις μπορείτε
β) Αποδείξτε ή απορρίψτε όσες από τις παρατηρήσεις γράψατε στο προηγούμενο ερώτημα.
Διερευνώντας τον περιγεγραμμένο κύκλο ενός τετραπλεύρου
Μπορείτε να βρείτε κύκλο ο οποίος να διέρχεται από τρία σημεία στο επίπεδο; Υπάρχουν προϋποθέσεις;
Μπορείτε να βρείτε κύκλο ο οποίος να διέρχεται από τέσσερα σημεία στο επίπεδο; Υπάρχουν προϋποθέσεις;
Η παρουσίαση:
Δείτε το φύλλο εργασίας εδώ.
Δείτε την τάξη εργασίας geogebraclassroom εδώ.
Δείτε τη διαδραστική ταινία για τα εγγράψιμμα τετράπλευρα εδώ:
Γεωμετρική άσκηση
Του Σωκράτη Ρωμανίδη
https://eisatopon.blogspot.com/2022/10/p-q-r-s.html
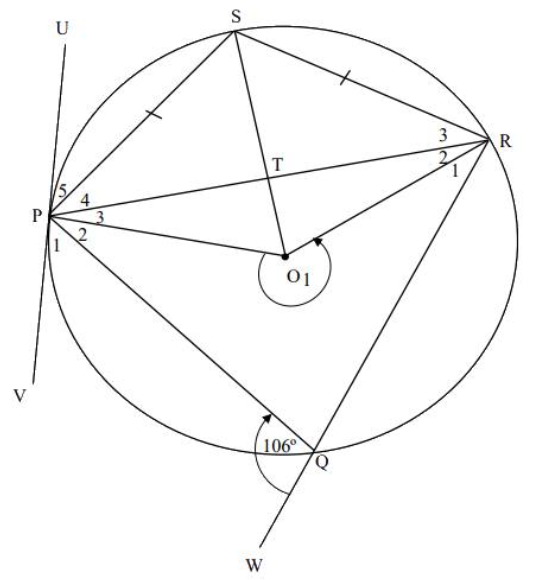
Στο παρακάτω σχήμα τα σημεία \(P, Q, R\) και \(S\) είναι σημεία σε κύκλο με κέντρο Ο. Η ευθεία UV είναι εφαπτομένη στον κύκλο στο σημείο P.Τα τμήματα PR και OS τέμνονται στο T και \( \widehat{PQW} =106^o\) και \( SP =SR \). Να υπολογισθούν οι γωνίες:
i) \( \widehat{PSR} \) ii) \( \widehat{R_3}\) iii) \( \widehat{P_5}\) iv) \( \widehat{O_1} \) v) \( \widehat{P_3}\)
Θεώρημα Poncelet-Steiner
Γεωμετρικές κατασκευές με κανόνα και «σκουριασμένο» διαβήτη !
https://en.wikipedia.org/wiki/Poncelet%E2%80%93Steiner_theorem
Κατασκευή Παράλληλης από σημείο εκτός ευθείες προς δοσμένη ευθεία ΑΒ με δοσμένο μέσο του ΑΒ
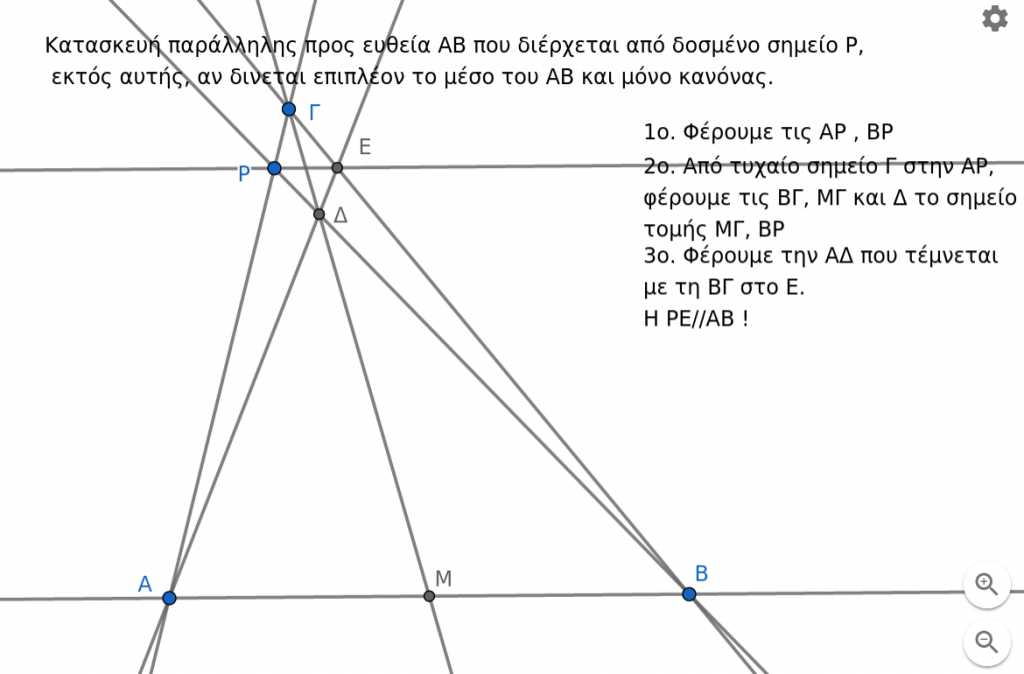
Δείτε την κατασκευή στο παρακάτω gifακι:

https://www.geogebra.org/geometry/mxvcjzuw?embed
Κατασκευή κάθετης προς ευθεία από δοσμένο σημείο.
https://www.geogebra.org/classic/zzquanan

Κατασκευή steiner ευθυγράμμου τμήματος σε δοσμένη ευθεία, με το μέσο του
https://www.geogebra.org/classic/becnhq6t
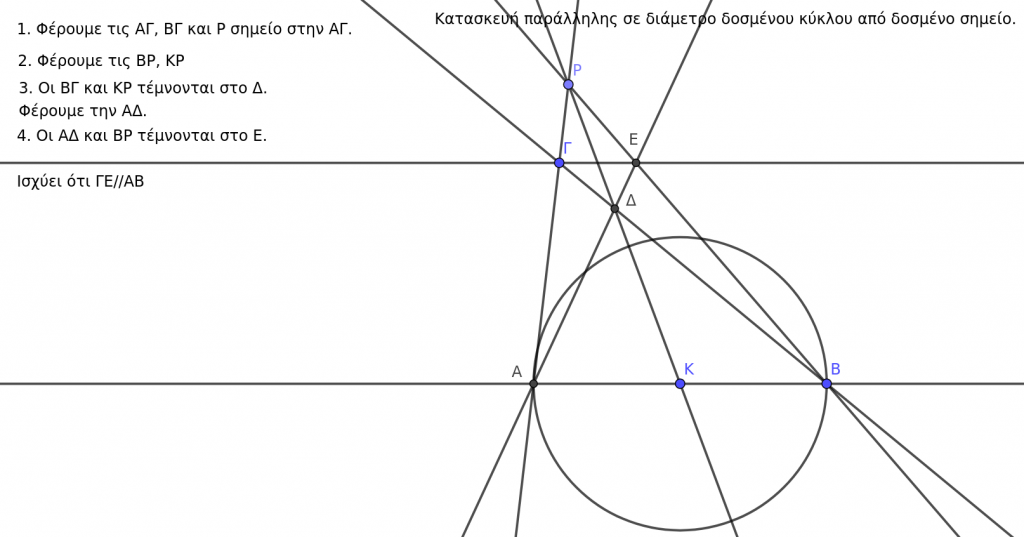
Κατασκευή Steiner παράλληλης από δοσμένο σημείο σε διάμετρο δοσμένου κύκλου.
https://www.geogebra.org/classic/mftdyqv3
The Poncelet-Steiner theorem says
Everything you can construct with a straightedge and a compass you can construct by the straightedge alone, provided you are given a circle and its center.
Motivated by Mascheroni’s result ↑ J.V.Poncelet conjectured this results in 1812��[1]��and it was proved by J.Steiner [2]��in 1833.
It can be shown that the constructions cannot be done by straightedge alone [3] . By the straightedge alone only the so called linear constructions can be done. For instance, using the straightedge alone, without a circle given, is not sufficient to construct square roots. Even simpler constructions as to half a straight line segment are impossible by the straightedge alone. Another example is the result known as Steiner’s theorem:
Steiner’s Theorem: It is impossible to find the center of a given circle with the straightedge alone.
The basic idea of the following proof goes back to Hilbert. If such a construction would be possible, then it would be preserved by projective transformations.��This due to the basic properties of projective transformation which preserve lines, objects constructible by the straightedge. On the other hand, the circle as a conic section is transformed to a conic section in general.��Even worse, the conjugate diameters 1 of a conic section pre-image may not be transformed to the conjugate diameters of the image. Consequently, the center of circle is not projected to the center of the image.
Άρθρο Poncelet-Steiner
33-Poncelet-Steiner-TheoremΕπιπλέον πηγές
Θέματα συμπληρωματικών Εισαγωγικών εξετάσεων Β λυκείου Προτύπου ΓΕΛ Ευαγγελικής Σχολής Σμύρνης Σεπτέμβριος 2021 – Υλικό Διδασκαλίας Σ.Χασάπη και άλλων συναδέλφων
Σταυρόλεξο στα τρίγωνα
202103033252 – Άθροισμα γωνιών – mathematica.gr
https://mathematica.gr/forum/viewtopic.php?p=335262&sid=9d8d03b42738b83dac90f0b1a98d20ff#p335262
Υπάρχει τρίγωνο ώστε το άθροισμα κάθε ζεύγους των γωνιών του να είναι μικρότερο των 120 μοιρών..?
Έστω \(x,y,z\) οι γωνίες ενός τριγώνου, με \(x+y+z=180^o\)
Ας υποθέσουμε ότι για αυτό το τρίγωνο ισχύει ότι το άθροισμα κάθε ζεύγους των γωνιών του είναι μικρότερα των \(120^o\).
Τότε όμως θα πρέπει να είναι
\(x+y<120^o, y+z<120^o, z+x<120^o\)
\( \Rightarrow 2(x+y+z)<360^o\)
\( \Rightarrow x+y+z<180^o \),
προφανώς άτοπο.
Δείτε στον αρχικό σύνδεσμο πολλές ακόμα όμορφες λύσεις!