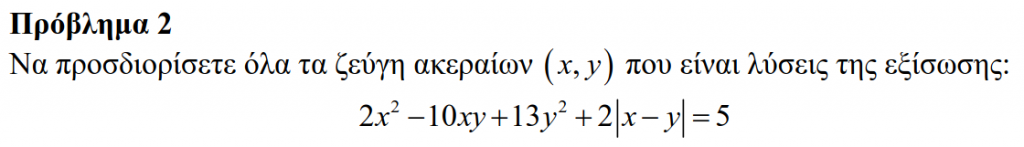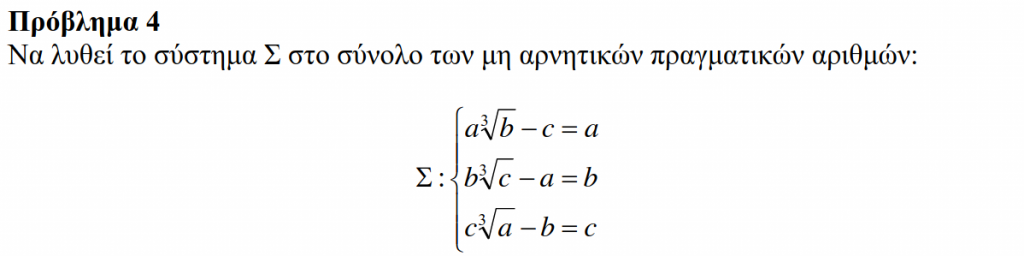
Κατηγορία: Β λυκείου
Θ2015Β2 – Γεωμετρία
Θ2014Β2
Κανόνας προσήμων του Descartes για πλήθος ριζών πολυωνύμων
Εισαγωγή στην εκθετική με συνεχή ανατοκισμό. Προσεγγίζοντας το e.
Ένας επενδυτής Α αποφασίζει να επενδύσει 500€ στην ΦΑΝΤΑΣΤΙΚΗ ΤΡΑΠΕΖΑ Α.Ε., η οποία του προσφέρει επιτόκιο 100% για ένα έτος.
Να βρείτε πόσα χρήματα θα εισπράξει συνολικά μετά από ένα έτος.
Με την αλλαγή του διευθυντή η ίδια τράπεζα του προσφέρει 50% επιτόκιο για ένα εξάμηνο για το ίδιο αρχικό ποσό.
Να βρείτε πόσα χρήματα θα εισπράξει μετά από ένα έτος με αυτούς τους όρους.
Ο επενδυτής σκέφτηκε να προτείνει στην τράπεζα να του δώσει το ίδιο επιτόκιο 100% κατ’αναλογία σε ημερήσιο επιτόκιο, δηλαδή \(\frac{100}{365} \)% για καθεμία από τις 365 ημέρες του χρόνου, σκεπτόμενος ότι ανάλογα με την προηγούμενη προσφορά θα βρεθεί κερδισμένος κατά πολύ περισσότερο.
Συμφωνείτε με αυτήν του τη σκέψη;
Θεώρημα Poncelet-Steiner
Γεωμετρικές κατασκευές με κανόνα και «σκουριασμένο» διαβήτη !
https://en.wikipedia.org/wiki/Poncelet%E2%80%93Steiner_theorem
Κατασκευή Παράλληλης από σημείο εκτός ευθείες προς δοσμένη ευθεία ΑΒ με δοσμένο μέσο του ΑΒ
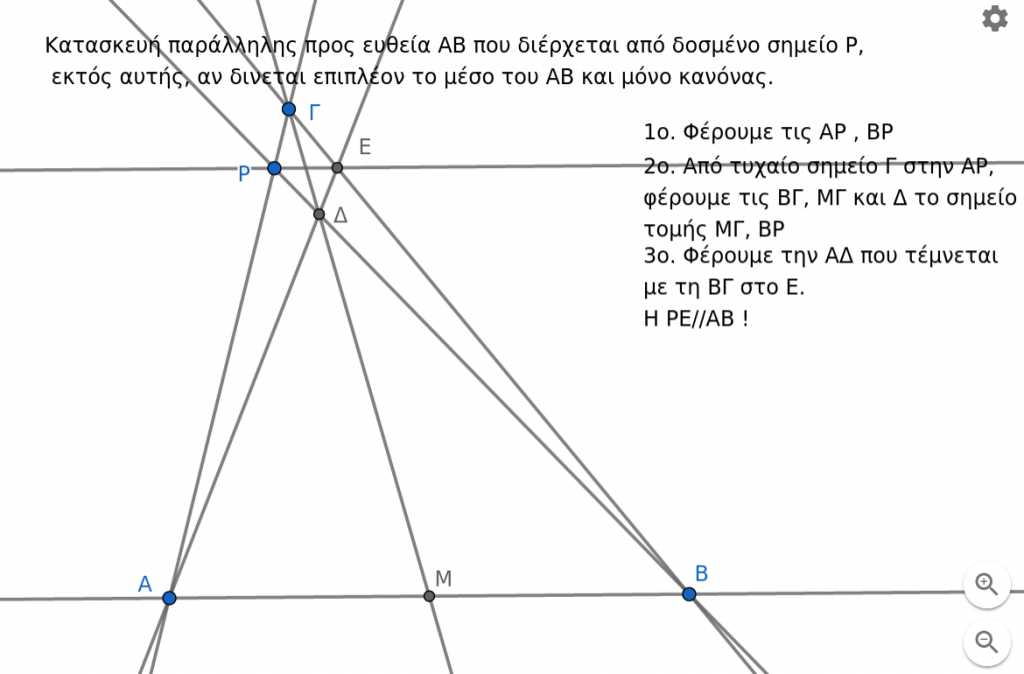
Δείτε την κατασκευή στο παρακάτω gifακι:

https://www.geogebra.org/geometry/mxvcjzuw?embed
Κατασκευή κάθετης προς ευθεία από δοσμένο σημείο.
https://www.geogebra.org/classic/zzquanan

Κατασκευή steiner ευθυγράμμου τμήματος σε δοσμένη ευθεία, με το μέσο του
https://www.geogebra.org/classic/becnhq6t
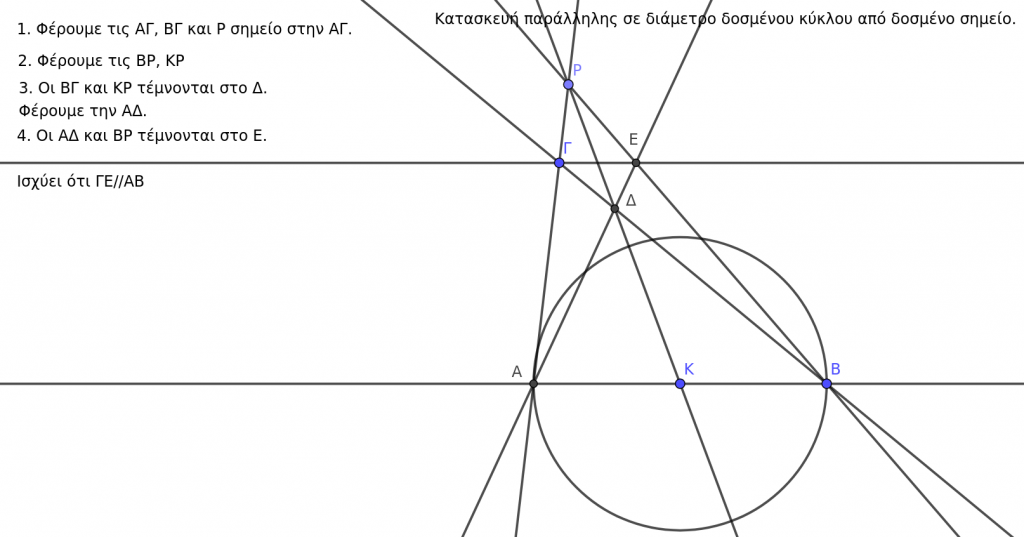
Κατασκευή Steiner παράλληλης από δοσμένο σημείο σε διάμετρο δοσμένου κύκλου.
https://www.geogebra.org/classic/mftdyqv3
The Poncelet-Steiner theorem says
Everything you can construct with a straightedge and a compass you can construct by the straightedge alone, provided you are given a circle and its center.
Motivated by Mascheroni’s result ↑ J.V.Poncelet conjectured this results in 1812��[1]��and it was proved by J.Steiner [2]��in 1833.
It can be shown that the constructions cannot be done by straightedge alone [3] . By the straightedge alone only the so called linear constructions can be done. For instance, using the straightedge alone, without a circle given, is not sufficient to construct square roots. Even simpler constructions as to half a straight line segment are impossible by the straightedge alone. Another example is the result known as Steiner’s theorem:
Steiner’s Theorem: It is impossible to find the center of a given circle with the straightedge alone.
The basic idea of the following proof goes back to Hilbert. If such a construction would be possible, then it would be preserved by projective transformations.��This due to the basic properties of projective transformation which preserve lines, objects constructible by the straightedge. On the other hand, the circle as a conic section is transformed to a conic section in general.��Even worse, the conjugate diameters 1 of a conic section pre-image may not be transformed to the conjugate diameters of the image. Consequently, the center of circle is not projected to the center of the image.
Άρθρο Poncelet-Steiner
33-Poncelet-Steiner-TheoremΕπιπλέον πηγές
Αριθμός επί διάνυσμα ή διάνυσμα επί αριθμό;
Έχει νόημα η δεύτερη πράξη;
ΠΡΟΦΑΝΩΣ και έχει νόημα, απλά δεν ορίζεται στο σχολικό βιβλίο κατεύθυνσης της β΄λυκείου. Στην εικόνα από το επισυναπτόμενο βιβλίο του Hungerford, Algebra, η τελευταία υπογραμμισμένη πρόταση αναφέρει:
Εκτός κι αν διευκρινίζεται διαφορετικά, κάθε πρότυπο επί ενός μεταθετικού δακτυλίου R, όπως είναι οι πραγματικοί αριθμοί, θα θεωρείται ότι αποτελεί αριστερό και δεξί πρότυπο με ra=ar, για κάθε r στο R , a στο A.
Αυτή είναι και η γενική τακτική, μεταξύ «αλγεβριστών» νομίζω…
Ένα πρότυπο (module) αποτελεί γενίκευση του διανυσματικού χώρου, αφού τα βαθμωτά θεωρούνται από έναν δακτύλιο γενικότερα και όχι απαραίτητα από το σώμα των πραγματικών αριθμών , όπως στο διανυσματικό χώρο. Αυτό που χαλάει είναι η προσεταιριστικότητα, γι αυτό και σε ασκήσεις που εμφανίζονται γενικά σε διάφορα βιβλία ζητείται να βρεθεί πχ αν ή πότε (ab)c = a(bc), όπου τα a,b,c είναι διανύσματα και θεωρούμε ότι η πράξη διάνυσμα επί αριθμό δίνει και έχει τις ίδιες ιδιότητες με την αριθμό επί διάνυσμα.
Το ακτίνιο Rad
Γραφικές παραστάσεις συναρτήσεων χωρίς απειροστικό λογισμό
του συναδέλφου Θανάση Ξένου
ΞένοςΓραφικέςπαραστάσειςσυναρτήσεων