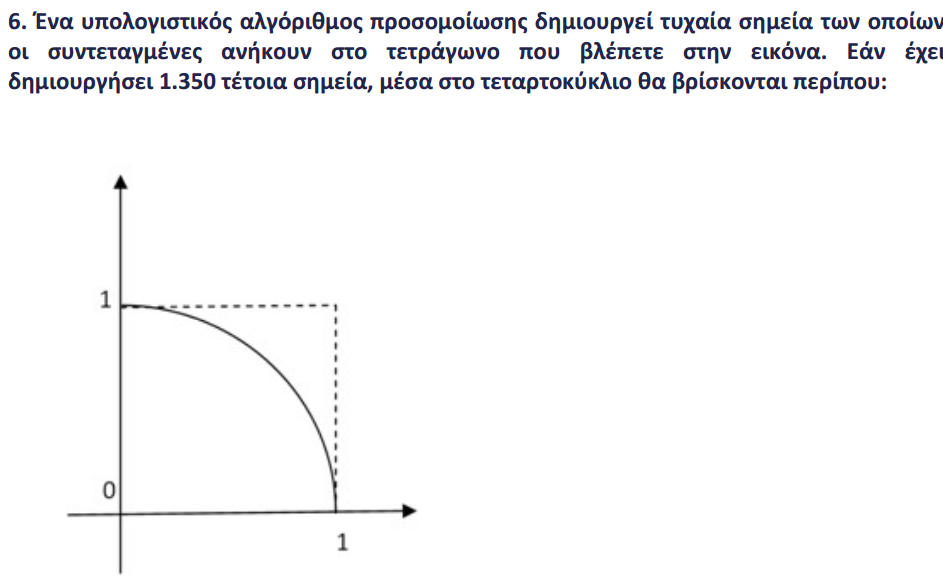
Το εμβαδόν του τετραγώνου είναι 1 τμ. Το εμβαδόν του τεταρτοκυκλίου είναι π/4 τμ.
Συνεπώς μέσα στο τεταρτοκύκλιο θα βρίσκονται π/4 * 1350 = 1059,75, δηλαδή 1060 σημεία.
Κατηγορία: Στατιστική
Στατιστική 2019Γ5
Στατιστική 2019Γ4
Τα ζεύγη που θα δημιουργηθούν και θα είναι τέλεια τετράγωνα είναι :
(2,4), (3,9), (4,16), (5,25), ( 6,36) , (7,49), (8,64), (9,81), (10,100) δηλαδή 9 συνολικά.
Όλα τα ζεύγη μαζί θα είναι όσα έχουν τον αριθμό 1 : 99 ζεύγη
όσα έχουν τον αριθμό 2 (χωρίς το 1) άρα : 98 ζεύγη
όσα έχουν τον αριθμό 3 (χωρίς τους 1,2), άρα: 97 ζεύγη
….
όσα έχουν τον αριθμό 98(χωρίς τους προηγούμενους),άρα: 2 ζεύγη
όσα έχουν τον αριθμό 99(χωρίς τους προηγούμενους),άρα: 1 ζεύγος.
Συνεπώς όλα τα ζεύγη θα είναι: 1+2+3+…+99, άθροισμα αριθμητικής προόδου 99 όρων: $$S_n = \frac{n(n+1}{2}, S_{99} = \frac{99\cdot 100}{2} = 4950$$
Και η πιθανόηττα θα είναι $$\frac{9}{4950} = 0,18%$$.
Συνεπώς η πιθανότητα να επιλεχθεί ένα τέτοιο ζεύγος θα είναι 99,82%.
