Απέμειναν προς διευθέτηση από εσάς:

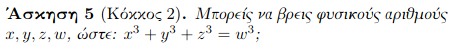
Πυθαγόρειες τριάδες και τελευταίο θεώρημα Φερμά σημειώσεις
mathcircle-a-2020-21-18aκαι αποδείξεις πλήρεις:
mathcircle-a-1820b-apodeikseisWordpress Συλλέκτης: Γρήγορη αρχειοθέτηση-δημοσίευση αντικειμένων και προσωπικών δημιουργιών από www.arithmoi.gr. Δίνει χρήσιμο υλικό διδασκαλίας εδώ: https://ylikodidaskalias.wordpress.com/ ΟΛΟ ΤΟ ΥΛΙΚΟ εδώ και σύνδεσμοι μόνο προς αυτό.
Απέμειναν προς διευθέτηση από εσάς:

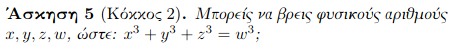
Πυθαγόρειες τριάδες και τελευταίο θεώρημα Φερμά σημειώσεις
mathcircle-a-2020-21-18aκαι αποδείξεις πλήρεις:
mathcircle-a-1820b-apodeikseisΈστω $a, b, c$ οι ρίζες της εξίσωσης $x^3-x-1=0$.
Να υπολογίσετε την τιμή της παράστασης:
$\frac{1-a}{1+a}+\frac{1-b}{1+b}+\frac{1-c}{1+c}$

Θέτουμε $t= \dfrac {1-x}{1+x}\,()$ , όπου $x$ ρίζα της δοθείσας τριτοβάθμιας. Λύνοντας την $()$ ως προς $x$ θα βρούμε $x= \dfrac {1-t}{1+t}$, οπότε θέτοντας στην τριτοβάθμια ισχύει
$\displaystyle{\left ( \dfrac {1-t}{1+t}\right )^3- \dfrac {1+t}{1-t} -1 =0}$
Πολλαπλασιάζοντας επί \((1-t)^3\) θα βρούμε μετά τις πράξεις $t^3-t^2+7t+1=0$. Από Vieta το άθροισμα των ριζών της τελευατίας είναι $1$. Αλλά από την $(*)$ οι ρίζες της τελευταίας είναι οι $\displaystyle{ \dfrac {1-a}{1+a}, \, \dfrac {1-b}{1+b},\, \dfrac {1-c}{1+c}}$. Συνεπώς
$\displaystyle{ \dfrac {1-a}{1+a}+ \dfrac {1-b}{1+b}+ \dfrac {1-c}{1+c}=1}$
Πρόκειται για εργασία που εκπονήθηκε ως φοιτητής.
Euler’s conjecture, a theory proposed by Leonhard Euler in 1769, hung in there for 200 years. Then L.J. Lander and T.R. Parkin came along in 1966, and debunked the conjecture in two swift sentences. Their article — which is now open access and can be downloaded here — appeared in the Bulletin of the American Mathematical Society. If you’re wondering what the conjecture and its refutation are all about, you might want to ask Cliff Pickover, the author of 45 books on math and science. He brought this curious document to the web last week.
Πηγή: The Shortest-Known Paper Published in a Serious Math Journal: Two Succinct Sentences | Open Culture
Σύντομες σημειώσεις, με στοιχεία και μεγαλύτερων τάξεων, για τους μαθητές που ενδιαφέρονται να αναζητήσουν…
5065202102043290-Χασάπης-Σωτήριος-Θεωρία-Αριθμών-για-το-Γυμνάσιο-2014