Του Σωκράτη Ρωμανίδη
https://eisatopon.blogspot.com/2022/10/p-q-r-s.html
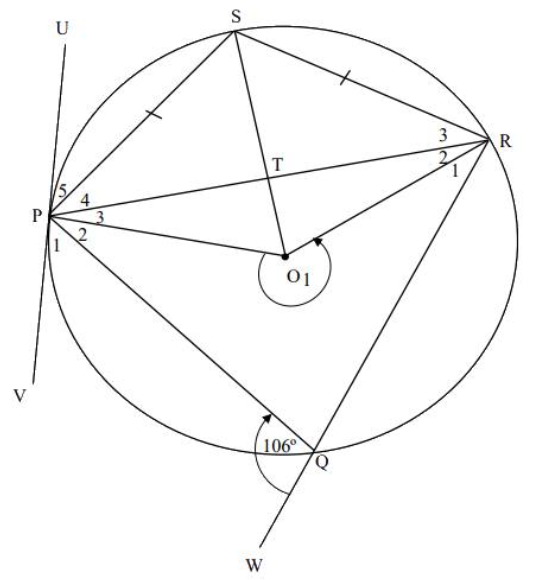
Στο παρακάτω σχήμα τα σημεία \(P, Q, R\) και \(S\) είναι σημεία σε κύκλο με κέντρο Ο. Η ευθεία UV είναι εφαπτομένη στον κύκλο στο σημείο P.Τα τμήματα PR και OS τέμνονται στο T και \( \widehat{PQW} =106^o\) και \( SP =SR \). Να υπολογισθούν οι γωνίες:
i) \( \widehat{PSR} \) ii) \( \widehat{R_3}\) iii) \( \widehat{P_5}\) iv) \( \widehat{O_1} \) v) \( \widehat{P_3}\)