
H σωστή απάντηση είναι η Δ.
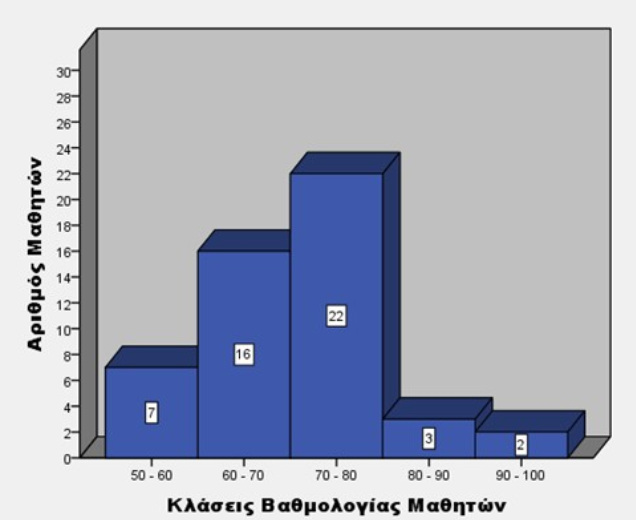
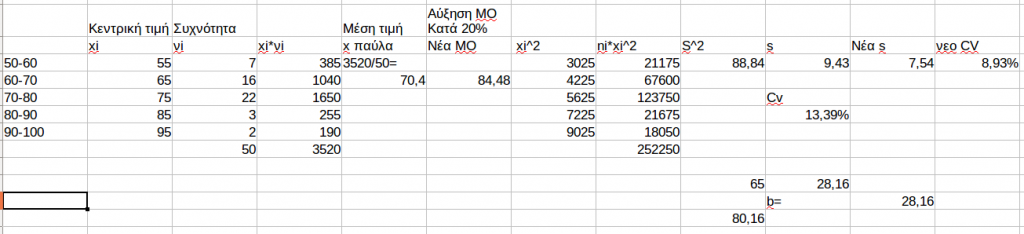
Διότι η μέση τιμή του δείγματος αρχικά βλέπουμε είναι 70,4.
Αύξηση 20% αυτής θα την κάνει 84,48.
Η $$s^2$$ του δείγματος είναι 88,84 και η s=9.43.
Μείωση 20% θα την κάνει 7,54.
Όμως για μεταβολή γραμμική έχουμε f(x) = ax + b
$$\overline{y} = a\cdot \overline{x} + b$$
και
$$s_y = |a| s_x$$
Έτσι προκύπτουν a=0,2 και b=28,16
Άρα το 65 θα γίνει 80,16.