Ετικέτα: γεωμετρία
omilos1021b10122021 Δύναμη Σημείου ως προς κύκλο και άλλα προβλήματα
Πόσο χαμηλά πέφτει;
https://mathematica.gr/forum/viewtopic.php?f=179&t=72448&p=351756#p351756
Πόσο χαμηλά θα πέσω ;
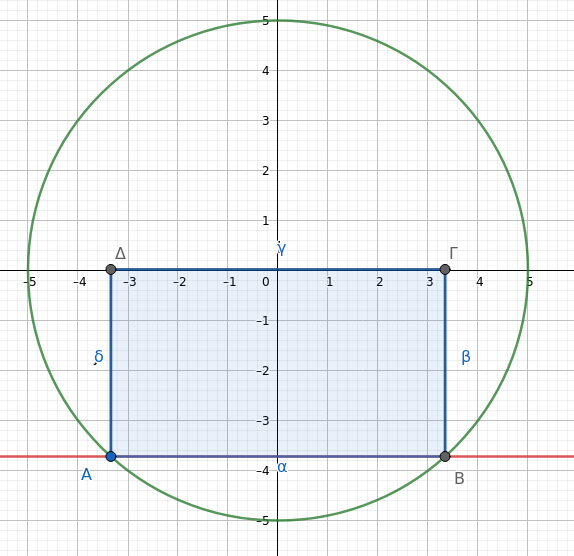
Μέσα σε κύκλο ακτίνας 
, με βάση την μεταβλητή οριζόντια χορδή 
, σχεδιάζω ορθογώνιο 
με εμβαδόν : 
. Πόσο ψηλά και – κυρίως – πόσο χαμηλά μπορεί να βρεθεί η πλευρά 
;
Υπόδειξη : Μην αναζητήσετε τον γεωμετρικό τόπο της κορυφής 
! 
Περιοδικό Εκθέτης 23 Η αναγκαιότητα ενίσχυσης της γεωμετρικής σκέψης στην Ελληνική Εκπαίδευση – Γιώργος Ρίζος
202103033252 – Άθροισμα γωνιών – mathematica.gr
https://mathematica.gr/forum/viewtopic.php?p=335262&sid=9d8d03b42738b83dac90f0b1a98d20ff#p335262
Υπάρχει τρίγωνο ώστε το άθροισμα κάθε ζεύγους των γωνιών του να είναι μικρότερο των 120 μοιρών..?
Έστω \(x,y,z\) οι γωνίες ενός τριγώνου, με \(x+y+z=180^o\)
Ας υποθέσουμε ότι για αυτό το τρίγωνο ισχύει ότι το άθροισμα κάθε ζεύγους των γωνιών του είναι μικρότερα των \(120^o\).
Τότε όμως θα πρέπει να είναι
\(x+y<120^o, y+z<120^o, z+x<120^o\)
\( \Rightarrow 2(x+y+z)<360^o\)
\( \Rightarrow x+y+z<180^o \),
προφανώς άτοπο.
Δείτε στον αρχικό σύνδεσμο πολλές ακόμα όμορφες λύσεις!
Γεωμετρία από Valdosta…
Αρχιμήδεια Στερεά
Κύκλοι και μέσο χορδής από σημείο επαφής.
Το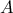 
είναι σημείο τομής των κύκλων : 
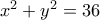και :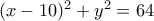 
.
Από το 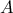διέρχεται μεταβλητή ευθεία , η οποία τέμνει τους δύο κύκλους στα σημεία 
.
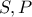Βρείτε την καρτεσιανή έκφραση του γεωμετρικού τόπου , του μέσου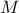 
του τμήματος 
.
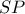Εικοσιδωδεκάεδρο 18 – Ασκήσεις γεωμετρίας Α΄λυκείου 2018
Κατεβάστε από εδώ.