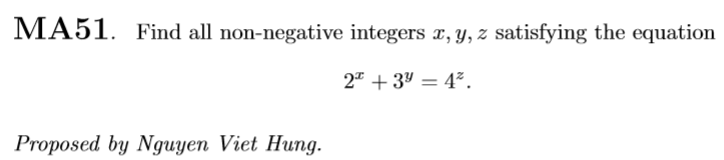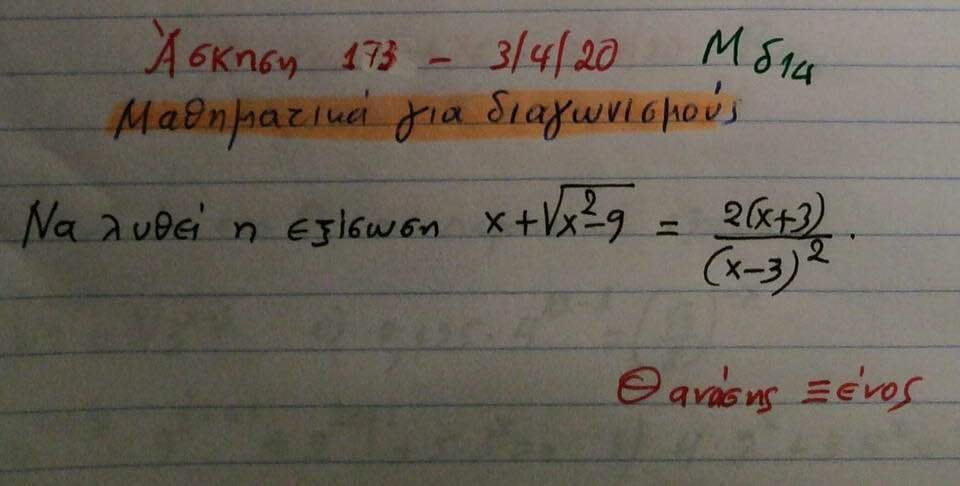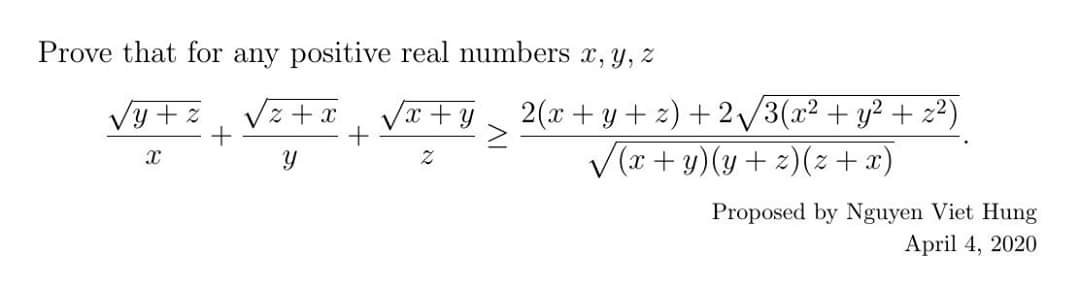Κατηγορία: Θεματικές κατηγορίες
Crux MA51
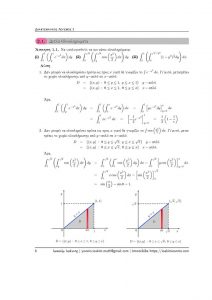
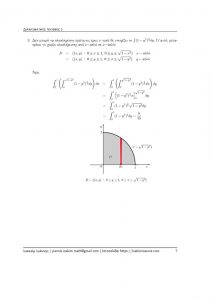
Yiannis Ioakim – Άσκηση στο διπλό ολοκλήρωμα
Πολλαπλή γραμμική παλινδρόμηση
Πηγή: 03_chapter02.pdf
Διερεύνηση των Προσδιοριστικών Παραγόντων και Μεθόδων Πρόβλεψης της Ζήτησης Ηλεκτρικής Ενέργειας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ
Διερεύνηση των Προσδιοριστικών Παραγόντων και Μεθόδων Πρόβλεψης της Ζήτησης Ηλεκτρικής Ενέργειας
ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Θεοχαρόπουλος Γεώργιος Επιβλέπων : Ιωάννης Ψαρράς Καθηγητής Ε.Μ.Π. Αθήνα, Ιούλιος 2015
Πηγή: DT2015-0218.pdf
Εξίσωση
Ανισότητα
Στατιστική 2019Γ6
Στατιστική 2019Γ5
Στατιστική 2019Γ4


Τα ζεύγη που θα δημιουργηθούν και θα είναι τέλεια τετράγωνα είναι :
(2,4), (3,9), (4,16), (5,25), ( 6,36) , (7,49), (8,64), (9,81), (10,100) δηλαδή 9 συνολικά.
Όλα τα ζεύγη μαζί θα είναι όσα έχουν τον αριθμό 1 : 99 ζεύγη
όσα έχουν τον αριθμό 2 (χωρίς το 1) άρα : 98 ζεύγη
όσα έχουν τον αριθμό 3 (χωρίς τους 1,2), άρα: 97 ζεύγη
….
όσα έχουν τον αριθμό 98(χωρίς τους προηγούμενους),άρα: 2 ζεύγη
όσα έχουν τον αριθμό 99(χωρίς τους προηγούμενους),άρα: 1 ζεύγος.
Συνεπώς όλα τα ζεύγη θα είναι: 1+2+3+…+99, άθροισμα αριθμητικής προόδου 99 όρων: $$S_n = \frac{n(n+1}{2}, S_{99} = \frac{99\cdot 100}{2} = 4950$$
Και η πιθανόηττα θα είναι $$\frac{9}{4950} = 0,18%$$.
Συνεπώς η πιθανότητα να επιλεχθεί ένα τέτοιο ζεύγος θα είναι 99,82%.