
Κατηγορία: Μαθηματικοί Όμιλοι
Αριθμητική modn
Ταυτότητα Διαίρεσης
pi day 2023 – Ημέρα π 2023

https://omilosmath.blogspot.com/2023/03/pi-day-event-14032023.html

Ιστορία του π
Διπλωματική της Παρασκευής Αρώνη: Ιστορία του π.











Τμήμα του βιβλίου του Beckmann μπορείτε να βρείτε δωρεάν εδώ.
Μερικά ταινιάκια και ένα τραγούδι για το π, θα βρείτε εδώ.
Ημέρα προσέγγισης του π
Εκτός της Ημέρας του πι, υπάρχει και η Ημέρα προσεγγίσεως του πι (Pi Approximation Day), στις 22 Ιουλίου κάθε χρόνου (22/7 με τον δικό μας τρόπο γραφής των ημερομηνιών), καθώς το κλάσμα 22/7 αποτελεί μία συνηθισμένη προσέγγιση του π, χρονολογούμενη από τον Αρχιμήδη.[4]
Υπολογίζοντας τα ψηφία του π…
Πόσα ψηφία μπορούμε να υπολογίσουμε;
Ένα εκατομμύριο ψηφία του π σε μία σελίδα εδώ.
Πόσα μπορείς να θυμάσαι; Παίξε εδώ.
Ρεκόρ υπολογισμού ψηφίων του π – 100 τρις ψηφία το 2022
http://314pimonth.blogspot.com/2023/03/2022.html
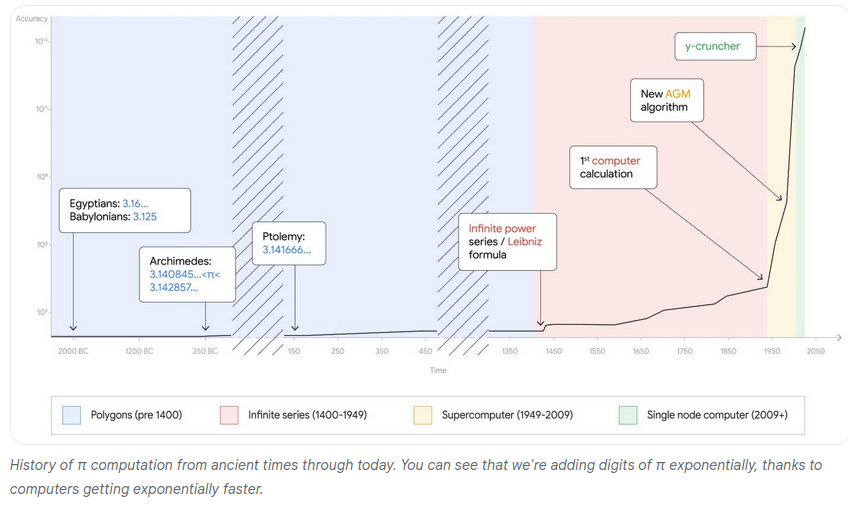
Παρουσίαση Υπολογίζοντας το π
Μέθοδοι και διαδικασίες υπολογισμού ανά τους αιώνες…
Δραστηριότητες για το π
Υπολογίζοντας το π με…ρίψη βελονών
https://mste.illinois.edu/activity/buffon/
Και εδώ πλήρης εξήγηση:
https://www.exploratorium.edu/snacks/pi-toss
pi-cut π-κόβοντας
https://www.exploratorium.edu/video/cutting-pi
Αναζητώντας ακολουθίες αριθμών στο π
https://www.angio.net/pi/piquery.html
Β΄λυκείου
Υπερβατικοί αριθμοί
Στοιχεία για το π…
25 στοιχεία για το π
Πηγή
1. The symbol for Pi has been in use for over 250 years. The symbol was introduced by William Jones, a Welsh mathematician, in 1706. The symbol was made popular by the mathematician Leonhard Euler.
2. Since the exact value of pi can never be calculated, we can never find the accurate area or circumference of a circle.
3. March 14 or 3/14 is celebrated as pi day because 3.14 are the first digits of pi. Math nerds around the world love celebrating this infinitely long, never-ending number.
4. The record for reciting the most number of decimal places of Pi was achieved by Rajveer Meena at VIT University, Vellore, India on 21 March 2015. He was able to recite 70,000 decimal places. To maintain the sanctity of the record, Rajveer wore a blindfold throughout the duration of his recall, which took an astonishing 10 hours! Can’t believe it? Well, here is the evidence.
5. Pi is actually a part of Egyptian mythology. People in Egypt believed that the pyramids of Giza were built on the principles of pi. The vertical height of the pyramids have the same relationship with the perimeter of their base as the relationship between a circle’s radius and its circumference. The pyramids are phenomenal structures and are one of the seven wonders of the world.
6. Physicist Larry Shaw started celebrating 14 March as Pi day at San Francisco’s Exploratorium science museum. There he is known as the Prince of Pi.
7. There is an entire language made from the number Pi. But how is that possible? Well, some people loved pi enough to invent a dialect based on it. In “Pi-lish” the number of letters in each word match the corresponding digit of pi. This first word has three letters, the second has one letter, the third has four letters, and so on. This language is more popular than you might think. Software engineer Michael Keith wrote an entire book, called Not a Wake in this language.
8. Pi wasn’t always known as pi. Before the 1700s, people referred to the number we know as pi as “the quantity which when the diameter is multiplied by it, yields the circumference”. Not surprisingly, people got tired of saying so much whenever they wanted to talk about Pi. The Welsh mathematician William Jones, a friend of Sir Isaac Newton, began using the symbol for pi in 1706.
9. We will never be able to find all the digits of pi because of its very definition as an irrational number. Babylonian civilization used the fraction 3 ⅛, the Chinese used the integer 3. By 1665, Isaac Newton calculated pi to 16 decimal places. Computers hadn’t been invented yet, so this was a pretty big deal. In the early 1700s Thomas Lagney calculated 127 decimal places of pi, reaching a new record. In the second half of the twentieth century, the number of digits of pi increased from about 2000 to 500,000 on the CDC 6600, one of the first computers ever made. This record was broken again in 2017 when a Swiss scientist computed more than 22 trillion digits of pi. The calculation took over a hundred days. Αυτό άλλαξε το 2022 όπως είδαμε, όταν υπολογίστικαν 100 τρις ψηφία του π στο google cloud.
10. The usefulness of pi has been a matter of debate, although it is loved by a lot of math enthusiasts. Some believe that tau (which amounts to 2π) is a better suited to circle calculations. For instance, you can multiply tau with the radius of a to calculate its circumference more intuitively. Tau/4 also represents the angle of a quarter of a circle.
11. In the Exploratorium science museum, a circular parade happens every year on pi day. Each person participating holds one digit in the number pi. It wasn’t celebrated around the United States like it is now until Congress passed Resolution 224, which designated March 14th as pi day. Congress hoped that celebrating pi day would cultivate a higher level of enthusiasm for math and science among American students.
12. The calculation of pi is a stress test for a computer. It works just like a digital cardiogram since it indicates the level of activity within the computer’s processor.
13. Givenchy sells a men’s cologne with the name ‘Pi’. The company markets this product as capable of enhancing the attractiveness of intelligent and visionary men.
14. The number pi is not just an important part of conversations among mathematicians or students. In the famous O.J. Simpson trial, the defense attorney and FBI agent’s argument revolved around the value of pi. The FBI agent’s findings in the case weren’t accurate because he used pi inaccurately.
15. The number pi was so alluring, even in the 16th century, that Dutch-German mathematician Ludolph van Ceulen spent most of his life calculating the first 36 digits of pi. It is said that the first 36 numbers were engraved on his tombstone, which is now lost.
16. William Shanks, a British mathematician, worked manually to find the digits of pi in 1873. He spent many years trying to calculate the pi digits by hand and found the first 707 digits. Unfortunately, the 527th digit he found was wrong, which made all the following digits wrong as well.
17. In the year 1888, an Indiana country doctor claimed that he had learned the exact measure of a circle through supernatural means. He believed in his “supernatural” knowledge so much that he filed a proposal to pass a bill in the Indiana legislature so that he could copyright his genius findings. However, there was a math professor in the legislature who showed the fellow how his proposed bill would result in a wrong value of pi.
18. The number pi is literally infinitely long. But the number 123456 doesn’t appear anywhere in the first million digits of pi. It is a bit shocking because if a million digits of pi don’t have the sequence 124356, it definitely is the most unique number.
19. Chinese people were far ahead of the West in finding the digits of pi. Why? Chinese mathematicians were ahead in the pi game because of two reasons: they had decimal notations and they had a symbol for the number zero. It wasn’t until the late middle ages that European mathematicians started using the number zero. At that time, European mathematicians partnered with Arab and Indian minds to bring the symbol of zero into their system.
20. In ancient times, mathematicians used a unique method to calculate pi. They would add more and more sides to a polygon so that its area approached the area of a circle. Archimedes, the most famous Greek mathematician and inventor, used a polygon with 96 sides. Many other mathematicians also used this polygon-method to compute the infinitely long number pi. In China, a mathematician used over 3,000 sides in a polygon to arrive at the value 3.14159. Another mathematician used about 25,000 sides to calculate pi.
21. Many mathematicians believe that it is more accurate to say that a circle has infinite corners than it is to say that it has none. It is only reasonable to assume that the infinite number of corners in a circle correlates to the infinite number of digits of pi.
22. The number pi is very effective when you used in calculations For instance, rounding the number pi to just 9 digits after the decimal and use it to calculate earth’s circumference yield incredibly accurate results. For every 25,000 miles, the number pi will only err to 1/4th of an inch.
23. Even today, people are racing to calculate more digits of pi in a never ending competition. In the year 2010, a Japanese engineer and an American computer wizard broke the record for the most number of pi digits by calculating up to 5 trillion digits of pi. The amazing part is that they didn’t use any supercomputers. They just used desktop computers, 20 external hard disks, and their brilliant minds.
24. The Greek letter π is the first letter of the word periphery and perimeter. And as we all know, pi is the ratio of a circle’s “periphery” to its diameter.
25. Interestingly, some of the most famous scientists in the world have a connection to pi day. Albert Einstein was born on March 14th, 1879. Stephen Hawking died on March 15th, 2018 at the age of 76.
Τυχαίοι αριθμοί το π
Ένας αριθμός καλείται κανονικός(normal), αν στα ψηφία του η πιθανότητα να πετύχουμε οποιοδήποτε ψηφίο στην αριθμητική του αναπαράσταση είναι ίδια για όλα τα ψηφία του αριθμητικού συστήματος αναπαραστάσης.
Το πρόβλημα αν το π είναι κανονικός αριθμός είναι ακόμα ανοικτό.
Comment: Pi might look random but it’s full of hidden patterns
Are the digits of pi random? (Berkley)
Βιβλιογραφία
Pi-related books
| The Joy of Pi – by David Blatner. A readable, fun story of the history of Pi and the stories of people obsessed with it. Includes suggestions for ways to memorize Pi and more. (144 pages; reading level: Young Adult and up.) |
| The Music of the Primes : Searching to Solve the Greatest Mystery in Mathematics – by Marcus Du Sautoy. A more in-depth, but still very approachable, discussion of the Riemann Hypothesis, one of the most important unanswered question about the fundamental nature of numbers. Not directly about Pi — but a great book for understanding more about some of the mysteries underlying numbers in general. (352 pages; reading level: Adult). |
| Sir Cumference and the Dragon of Pi (A Math Adventure) is a fun math-inspired fairy tale about a boy whose father drinks a potion that turns him into a dragon. The son must use math to restore him to normal. Late elementary school, but perhaps fun for middle school as well. Illustrated. Part of a larger series of math adventures. |
| Piece of Pi: Wit-Sharpening, Brain-bruising, Number-Crunching Activites with Pi (Grades 6-8). Pretty much what it sounds like. 🙂 Activities and challenges to explore Pi in the world. |
Χριστουγεννιάτικες ευχές 2022-23

Κάρτες ευχετήριες από τον Όμιλο Μαθηματικών του Πειραματικού Λυκείου Πανεπιστημίου Μακεδονίας, από τον σύνδεσμο:
Στο πλαίσιο της συνεργασίας του Ομίλου Μαθηματικών του Πειραματικού Λυκείου του Πανεπιστημίου Μακεδονίας με το NOESIS-Κέντρο Διάδοσης Επιστημών και Μουσείο Τεχνολογίας, προσφέρουμε δωρεάν στην εκπαιδευτική κοινότητα και στο ευρύ κοινό χριστουγεννιάτικες κάρτες με μαθηματικές-εικαστικές δημιουργίες για να στείλετε τις χριστουγεννιάτικες ευχές σας.
Οι κάρτες βασίζονται σε έργα που σχεδιάστηκαν από τους μαθητές και τις μαθήτριες του Ομίλου Μαθηματικών και απεικονίζουν Χριστουγεννιάτικα δέντρα που είναι εμπνευσμένα από την τέχνη του ψηφιδωτού. Τα έργα αξιοποιούν στον σχεδιασμό τους τις μαθηματικές ιδέες των Ισομετριών και των Ψηφιδώσεων (πλακοστρώσεων/tessellations), που έπαιξαν σημαντικό ρόλο στις τέχνες όλων των πολιτισμών που άκμασαν στον πλανήτη από τις απαρχές του προϊστορικού ανθρώπου μέχρι σήμερα και είναι χρωματισμένα σε θερμούς φθινοπωρινούς, παγωμένους χειμωνιάτικους και λαμπερούς γιορτινούς χρωματικούς συνδυασμούς.
Τις κάρτες μπορείτε να κατεβάσετε από αυτή την ιστοσελίδα. Μπορείτε να τις χρησιμοποιήσετε σε ηλεκτρονική μορφή ή και να τις τυπώσετε. Κάνοντας κλικ πάνω στην κάρτα που σας αρέσει θα ανοίξει η κάρτα στο Drive και από εκεί μπορείτε να κάνετε Λήψη/Download. Οι κάρτες διατίθενται, είτε χωρίς κείμενα για να γράψετε εσείς τις ευχές που θέλετε, είτε με χριστουγεννιάτικες ευχές, στα ελληνικά και στα αγγλικά. Περιηγηθείτε στις διάφορες σελίδες και επιλέξτε ότι σας αρέσει και σας εκφράζει.
Παράγωγοι και μερικές παράγωγοι.
Η έννοια της παραγώγου για πραγματική συνάρτηση μίας μεταβλητής
Ο λόγος μεταβολής μίας συνάρτησης και η μέση ταχύτητα
Το όριο του λόγου μεταβολής και η στιγμιαία ταχύτητα
Συναρτήσεις πολλών μεταβλητών
Γεωμετρία πραγματικών συναρτήσεων πολλών μεταβλητών
Επιφάνειες δευτέρου βαθμού: https://www.esofia.net/sites/default/files/indicative-capital/ch1.pdf
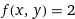
https://www.wolframalpha.com/input?key=&i=f%28x%2Cy%29%3D2
Γενική μορφή επιπέδου z = ax + by +c
https://www.geogebra.org/calculator/bfeauhhf
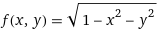
https://www.wolframalpha.com/input?key=&i=f%28x%2Cy%29%3Dsqrt%281-x%5E2+-+y%5E2+%29
https://www.geogebra.org/3d/shfangtz
καμπύλες στάθμης
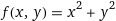
https://www.wolframalpha.com/input?key=&i=f%28x%2Cy%29%3Dx%5E2+%2B+y%5E2
https://www.geogebra.org/m/jccuqfun
https://www.geogebra.org/classic/jccuqfun
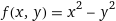
https://www.wolframalpha.com/input?key=&i=f%28x%2Cy%29+%3D+x%5E2+-+y%5E2
https://www.geogebra.org/3d/hdkazcav
Κωνικές τομές
https://www.geogebra.org/3d/da9ks7uw
Ισοϋψείς καμπύλες
Κατευθυνόμενη παράγωγος
Η κατευθυνόμενη παράγωγος στη διεύθυνση ενός διανύσματος u είναι το εσωτερικό γινόμενο της κλίσης grad με το διάνυσμα u
Εύρεση κατεύθυνσης με μέγιστη πτώση…
Αν η κλίση είναι διαφορετική του 0, τότε δείχνει προς εκείνη την κατεύθυνση κατά μήκος της οποίας η συνάρτηση αυξάνεται ταχύτερα.
Ενώ η αντίθετη της κλίσης δείχνει την κατεύθυνση προς την οποία φθίνει γρηγορότερα.
ΕΦαπτόμενο επίπεδο
ΤΟ εφαπτόμενο επίπεδο στο (x0,y0) έχει εξίσωση:
κλίση f(x0,y0) . (x-x0 , y-y0) = 0
Εύρεση ακροτάτων
Δύο κορυφές
Μπουκάλι Klein bottle

Στην τοπολογία, ένα κλάδο των μαθηματικών, η Φιάλη του Κλάιν ή το Μπουκάλι του Κλάιν, είναι ένα παράδειγμα μιας μη-προσανατολιζόμενης επιφάνειας. Είναι μια δισδιάστατη πολλαπλότητα πάνω στην οποία δεν μπορεί να οριστεί ένα σύστημα για τον προσδιορισμό ενός κάθετου διανύσματος. Με απλά λόγια, είναι μια μονόπλευρη επιφάνεια στην οποία, αν περπατήσει κανείς επάνω της, θα μπορούσε να φτάσει στο σημείο στο οποίο ξεκίνησε, αλλά ανάποδος, δηλαδή με το κεφάλι να είναι προς την κατεύθυνση την οποία ήταν τα πόδια του. Άλλα μη-προσανατολιζόμενα αντικείμενα περιλαμβάνουν τη λωρίδα του Μέμπιους και το πραγματικό προβολικό επίπεδο. Ενώ μια λωρίδα του Μέμπιους είναι μια επιφάνεια με σύνορο, η φιάλη του Κλάιν δεν έχει σύνορο (για σύγκριση, μια σφαίρα είναι μια προσανατολιζόμενη επιφάνεια χωρίς σύνορο).
Η φιάλη του Κλάιν περιγράφηκε για πρώτη φορά το 1882 από τον Γερμανό μαθηματικό Φέλιξ Κλάιν. Είναι πιθανό να είχε ονομαστεί αρχικά ως η επιφάνεια του Κλάιν (“Kleinsche Fläche“) και στη συνέχεια να παρερμηνεύτηκε ως η φιάλη του Κλάιν (“Kleinsche Flasche“), η οποία μπορεί να οδήγησε τελικά στην υιοθέτηση αυτού του όρου και στη γερμανική γλώσσα.[1]
In topology, a branch of mathematics, the Klein bottle is an example of a non-orientable surface; it is a two-dimensional manifold against which a system for determining a normal vector cannot be consistently defined.
In practical terms, they are remarkably difficult to fill with water!
Ένα Ιδιότυπο μπιλιάρδο
του Νίκου Μαυρογιάννη από εδώ https://www.facebook.com/100009159791448/videos/489384459832332/
Έχουμε ένα σημείο Α(0,a) στον θετικό ημιάξονα των y. Μας ενδιαφέρει να βρούμε μια συνάρτηση ορισμένη στο R που παίρνει θετικές τιμές με την ακόλουθη ιδιότηταΑν από οποιοδήποτε σημείο X του άξονα των x σκοπεύσουμε το Α η ανακλώμενη στην γραφική παράστασαη της f να είναι κάθετη στον στον άξονα των x. Mια μερική απάντηση μπορεί να δοθεί με ύλη Β’ Λυκείου: Αρκει να πάρουμε μια παραβολή y=cx²+d (c, d θετικά) με εστία το A και να αξιοποιήσουμε την ανακλαστική ιδιότητα της. Η γενική απάντηση είναι πιο εκτεταμένη. Απαιτεί την επίλυση της διαφορικής εξισώσης x(y’)²-2yy’+2ay’-x=0 η οποία είναι τύπου Lagrange. Ωστόσο με κάποια “υποστηρίγματα” μπορεί να λυθεί με ύλη Γ Λυκείου. Ενδιαφέρον είναι ότι δημιουργείται με παιγνιώδη τρόπο η 1-1 και επί απεικόνιση Χ→Υ που απεικονίζει το R σε ένα ανοικτό διάστημα αποδεικνύοντας ότι είναι ισοπληθικά (φυσικά αυτό γίνεται και αλλιώς λ.χ. με την y=tanx η την y=x/(1+|x|)).Επίσης ενδιαφέρον παρουσιάζει και η κατασκευή του μπιλιάρδου στην Geobebra όπου κάποια ζητηματα με την ρύθμιση της τροχιάς και την ταχύτητα τη μπίλιας είναι διδακτικά. Θα μπορούσε να αποτελέσει βάση για σχολική εργασία όπου δίνεται η ευκαιρία να έλθουν τα παιδιά σε επαφή με ιδέες των εικονιζομένων (Απολλώνιος, Johann Bernoulli, Lagrange, Cantor).
https://www.facebook.com/nsmavrogiannis/videos/489384459832332/
Μαθηματικές…συμπτώσεις
Είναι ενδιαφέρον θέμα οι Μαθηματικές συμπτώσεις, δηλαδή σχέσεις – ιδέες που φαίνονται να ισχύουν ή να ισχύουν, αλλά να μην έχουν μαθηματικό λόγο να ισχύουν.
https://www.facebook.com/photo/?fbid=5129033793884177&set=gm.3325323091022644


