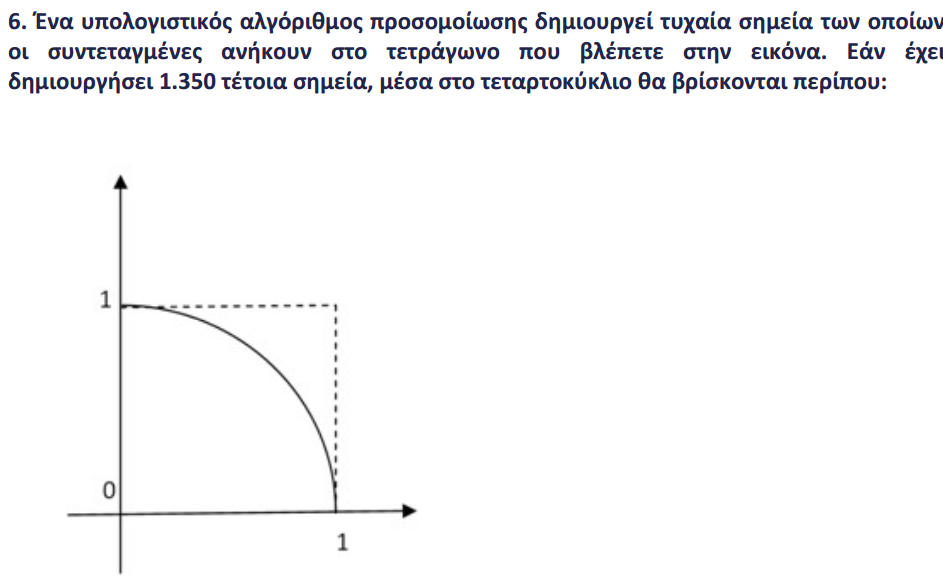
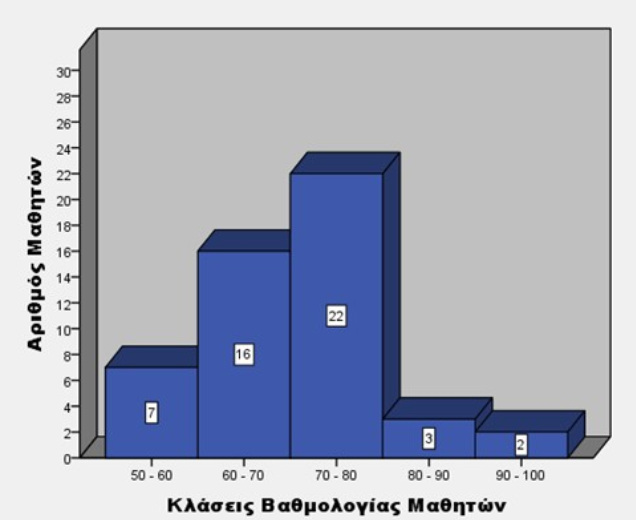
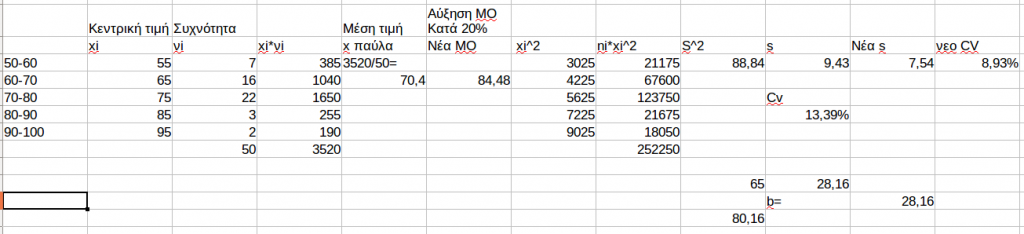
Πηγή: instructions.pdf
1 Πρόταση Αξιοποίησης Υφιστάμενης Υποδομής Για Πραγματοποίηση Μαθημάτων Μέσω Διαδικτύου Project: «Έγινε Παράδοση!» Στο διαδίκτυο παρέχονται πλέον αμέτρητες πλατφόρμες δωρεάν φιλοξενίας συγχρονισμένης διδασκαλίας. Στο 2ο Πειραματικό Λύκειο Αθήνας, αξιοποιήσαμε τη zoom.us. Με την είσοδό μας στον δικτυακό τόπο της πλατφόρμας, μας δίνεται η δυνατότητα δωρεάν εγγραφής, πατώντας στο SIGN UP, IT’S FREE!. 2 Έτσι, μεταβαίνουμε στην οθόνη: Εδώ, μας δίνεται η δυνατότητα να συνδεθούμε: • είτε με εγγραφή με χρήση του email μας • είτε μέσω του λογαριασμού Google που διαθέτουμε • είτε με χρήση του λογαριασμού Facebook που ενδεχομένως έχουμε Στην περίπτωση χρήσης του email μας, το εισάγουμε στο κατάλληλο κελί και πατάμε Confirm. 3 Απαιτείται ένα επιπλέον βήμα, αυτό της επιβεβαίωσης του λογαριασμού μας. (Πρακτικά μετά την εγγραφή μας, η πλατφόρμα αποστέλλει στον λογαριασμό μας ένα email επιβεβαίωσης, στο οποίο περιέχεται ένας σύνδεσμος. Όταν πατήσουμε σε αυτόν, ενεργοποιείται ο λογαριασμός μας στην πλατφόρμα). 4 Μόλις ολοκληρωθεί η εγγραφή μας (και η ενδεχόμενη επαλήθευση του λογαριασμού), μεταβαίνουμε στην ακόλουθη οθόνη: Εδώ πλέον εισάγουμε το όνομα, το επώνυμο και το password που έχουμε διαλέξει και πατάμε Continue. (To password το ζητάει δύο φορές, για να επιβεβαιωθεί ότι το έχουμε καταχωρίσει ορθά). Πλέον, η οθόνη που έχουμε μπροστά μας είναι η ακόλουθη: 5 Σε αυτή, μας καλεί να εισάγουμε τρία email φίλων μας, ώστε να τους προτείνουμε να εγγραφούν στην πλατφόρμα. Τέλος, κάνουμε κλικ στο κελί “I’m not a robot” και πατάμε Invite. Τώρα, η οθόνη μας είναι αυτή: Σε αυτή, φαίνεται ο σύνδεσμος (url) για τον «χώρο» της δικτυακής μας τάξης. Κάνουμε κλικ στο Start a Meeting Now. 6 Τώρα θα σας ζητηθεί να «κατεβάσετε» την εφαρμογή της zoom, ώστε να μπορείτε να αξιοποιείται την πλατφόρμα. Εγκαταστήστε την και κατόπιν συναινέστε στην άδεια χρήσης του μικροφώνου και της κάμεράς σας από την εφαρμογή. Είστε έτοιμοι! Όταν θέλετε να προσκαλέσετε τους μαθητές σας, αρκεί να τους κοινοποιήσετε το url της τάξης σας. Πρακτικό είναι να χρησιμοποιείτε τη λειτουργία share screen, γιατί με αυτή, όσα γράφετε στον υπολογιστή σας, το βλέπουν άμεσα και οι μαθητές σας. Αν ενεργοποιήσετε αυτή τη λειτουργία, μην ξεχάσετε στο παράθυρο: 7 να ενεργοποιήσετε τη λειτουργία Share computer sound και Optimize Screen Sharing for video clip. Πατήστε Share. Όλα είναι έτοιμα! Μπορείτε να προγραμματίζετε τα meeting σας, να προκαθορίζετε τη διάρκειά τους, να συνομιλείτε ζωντανά με τους μαθητές, με εικόνα, ήχο και γραπτά, να διαμοιράζεστε αρχεία. Όσο έχετε κέφι, τόσο βρίσκετε δυνατότητες… Καλή αποστειρωμένη διαμονή στο σπίτι, Με τιμή, Σ. Ασημέλλης