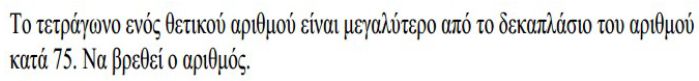Ετικέτα: προβλήματα
Ένα Ιδιότυπο μπιλιάρδο
του Νίκου Μαυρογιάννη από εδώ https://www.facebook.com/100009159791448/videos/489384459832332/
Έχουμε ένα σημείο Α(0,a) στον θετικό ημιάξονα των y. Μας ενδιαφέρει να βρούμε μια συνάρτηση ορισμένη στο R που παίρνει θετικές τιμές με την ακόλουθη ιδιότηταΑν από οποιοδήποτε σημείο X του άξονα των x σκοπεύσουμε το Α η ανακλώμενη στην γραφική παράστασαη της f να είναι κάθετη στον στον άξονα των x. Mια μερική απάντηση μπορεί να δοθεί με ύλη Β’ Λυκείου: Αρκει να πάρουμε μια παραβολή y=cx²+d (c, d θετικά) με εστία το A και να αξιοποιήσουμε την ανακλαστική ιδιότητα της. Η γενική απάντηση είναι πιο εκτεταμένη. Απαιτεί την επίλυση της διαφορικής εξισώσης x(y’)²-2yy’+2ay’-x=0 η οποία είναι τύπου Lagrange. Ωστόσο με κάποια “υποστηρίγματα” μπορεί να λυθεί με ύλη Γ Λυκείου. Ενδιαφέρον είναι ότι δημιουργείται με παιγνιώδη τρόπο η 1-1 και επί απεικόνιση Χ→Υ που απεικονίζει το R σε ένα ανοικτό διάστημα αποδεικνύοντας ότι είναι ισοπληθικά (φυσικά αυτό γίνεται και αλλιώς λ.χ. με την y=tanx η την y=x/(1+|x|)).Επίσης ενδιαφέρον παρουσιάζει και η κατασκευή του μπιλιάρδου στην Geobebra όπου κάποια ζητηματα με την ρύθμιση της τροχιάς και την ταχύτητα τη μπίλιας είναι διδακτικά. Θα μπορούσε να αποτελέσει βάση για σχολική εργασία όπου δίνεται η ευκαιρία να έλθουν τα παιδιά σε επαφή με ιδέες των εικονιζομένων (Απολλώνιος, Johann Bernoulli, Lagrange, Cantor).
https://www.facebook.com/nsmavrogiannis/videos/489384459832332/
Πόσο χαμηλά πέφτει;
https://mathematica.gr/forum/viewtopic.php?f=179&t=72448&p=351756#p351756
Πόσο χαμηλά θα πέσω ;
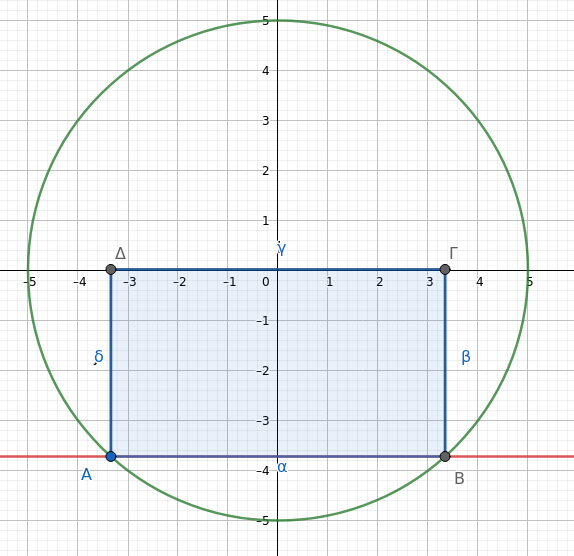
Μέσα σε κύκλο ακτίνας  , με βάση την μεταβλητή οριζόντια χορδή
, με βάση την μεταβλητή οριζόντια χορδή  , σχεδιάζω ορθογώνιο
, σχεδιάζω ορθογώνιο 
με εμβαδόν :  . Πόσο ψηλά και – κυρίως – πόσο χαμηλά μπορεί να βρεθεί η πλευρά
. Πόσο ψηλά και – κυρίως – πόσο χαμηλά μπορεί να βρεθεί η πλευρά  ;
;
Υπόδειξη : Μην αναζητήσετε τον γεωμετρικό τόπο της κορυφής  !
! ![]()
Θ2009Α1A
Θ2007Α1Α
Πρόβλημα ημέρας Ομίλου Μαθηματικών 11/03/2022
Τα προβλήματα στα Μαθηματικά Γ΄λυκείου
https://grafis.sch.gr/index.php/s/4MIs3fKEeRbmO77/download
του συναδέλφου Λευτέρη Ευθυμίου.
Τα-Προβλήματα-στα-Μαθκά-Προσα