Ετικέτα: Στατιστική
Στατιστική 2019Γ6
Στατιστική 2019Γ5
Στατιστική 2019Γ4


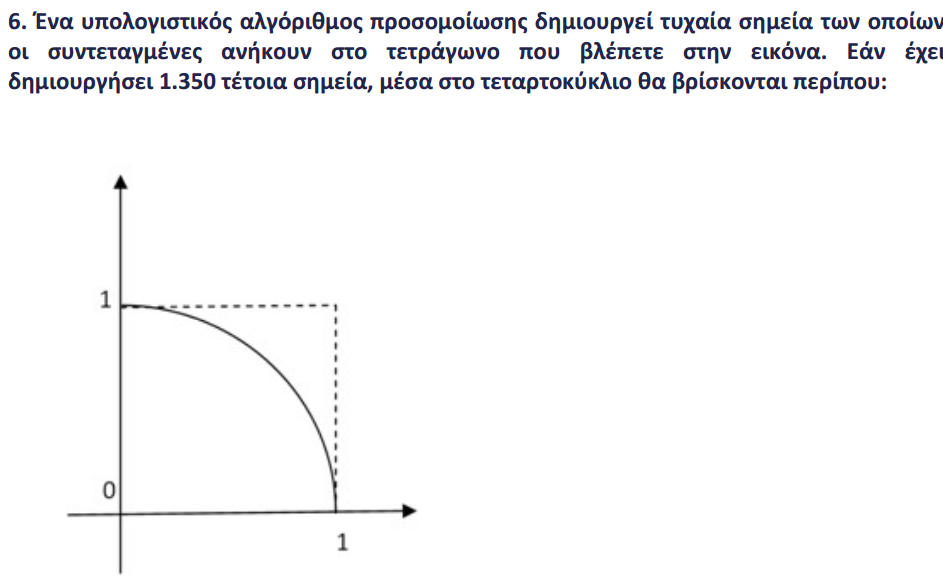
Τα ζεύγη που θα δημιουργηθούν και θα είναι τέλεια τετράγωνα είναι :
(2,4), (3,9), (4,16), (5,25), ( 6,36) , (7,49), (8,64), (9,81), (10,100) δηλαδή 9 συνολικά.
Όλα τα ζεύγη μαζί θα είναι όσα έχουν τον αριθμό 1 : 99 ζεύγη
όσα έχουν τον αριθμό 2 (χωρίς το 1) άρα : 98 ζεύγη
όσα έχουν τον αριθμό 3 (χωρίς τους 1,2), άρα: 97 ζεύγη
….
όσα έχουν τον αριθμό 98(χωρίς τους προηγούμενους),άρα: 2 ζεύγη
όσα έχουν τον αριθμό 99(χωρίς τους προηγούμενους),άρα: 1 ζεύγος.
Συνεπώς όλα τα ζεύγη θα είναι: 1+2+3+…+99, άθροισμα αριθμητικής προόδου 99 όρων: $$S_n = \frac{n(n+1}{2}, S_{99} = \frac{99\cdot 100}{2} = 4950$$
Και η πιθανόηττα θα είναι $$\frac{9}{4950} = 0,18%$$.
Συνεπώς η πιθανότητα να επιλεχθεί ένα τέτοιο ζεύγος θα είναι 99,82%.
Στατιστική 2019Γ3

Θεωρούμε το ενδεχόμενο Α= {η ρίψη του ζαριού φέρει 1}
Τότε A’ = { Η ρίψη του ζαριού δεν είναι 1}.
P(A)= 1/6 και P(A’)= 5/6
Αν επαναλάβουμε το πείραμα ν φορές τότε η πιθανότητα να μην έρθει κανένα ένα στις ν φορές θα είναι P(A’ A’ A’ ….A’) ν φορές δηλαδή $$P(A’) P(A’)…P(A’) = (5/6)^ν$$
Συνεπώς η πιθανότητα να έρθει 1 μετά από ν φορές θα είναι:
$$1 – \left(\frac{5}{6}\right)^n = 0,99 \Leftrightarrow \left(\frac{5}{6}\right)^n = 0,01 \Leftrightarrow n\ln(5/6) = \ln(0,01) \Leftrightarrow n = 25.26$$
Άρα πρέπει να γίνουν 26 ρίψεις.
Θέμα Στατιστικής 2019Λ2

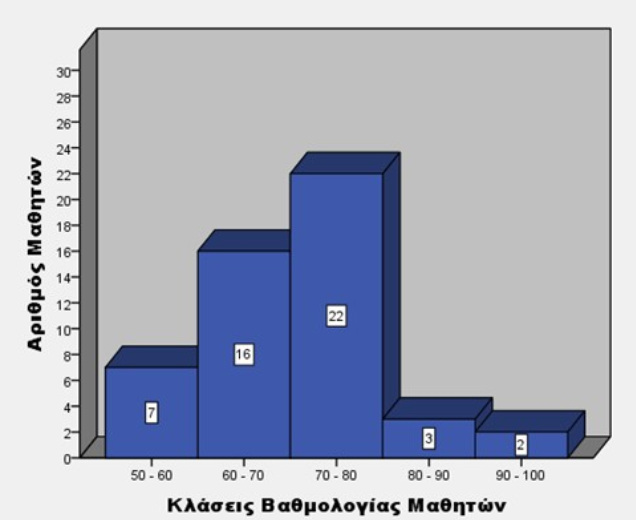

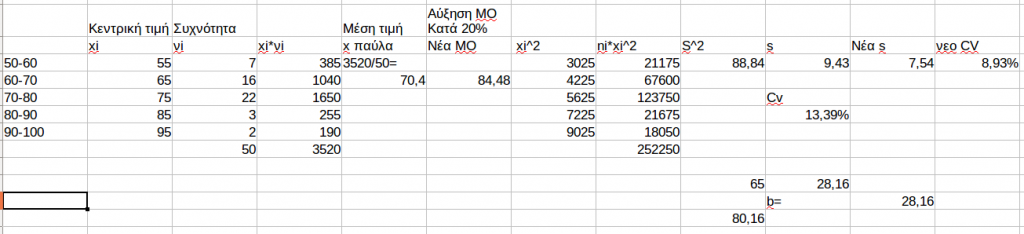
H σωστή απάντηση είναι η Δ.
Διότι η μέση τιμή του δείγματος αρχικά βλέπουμε είναι 70,4.
Αύξηση 20% αυτής θα την κάνει 84,48.
Η $$s^2$$ του δείγματος είναι 88,84 και η s=9.43.
Μείωση 20% θα την κάνει 7,54.
Όμως για μεταβολή γραμμική έχουμε f(x) = ax + b
$$\overline{y} = a\cdot \overline{x} + b$$
και
$$s_y = |a| s_x$$
Έτσι προκύπτουν a=0,2 και b=28,16
Άρα το 65 θα γίνει 80,16.