Wordpress Συλλέκτης: Γρήγορη αρχειοθέτηση-δημοσίευση αντικειμένων και προσωπικών δημιουργιών από www.arithmoi.gr. Δίνει χρήσιμο υλικό διδασκαλίας εδώ: https://ylikodidaskalias.wordpress.com/ ΟΛΟ ΤΟ ΥΛΙΚΟ εδώ και σύνδεσμοι μόνο προς αυτό.
Περιγραφή της δραστηριότητας εδώ
και μία όμορφη και κατανοητή εξήγηση εδώ.
Εικόνες από την εφαρμογή σε τρία τμήματα(Α2,Β3,ΓΘ2) το 2022
Πηγή: Όμιλος Μαθηματικών Προτύπου ΓΕΛ Ευαγγελικής Σχολής Σμύρνης : Μετρώντας το π…με σπίρτα (Ημέρα π 2022)
Εικασία Catalan – Θεώρημα Mihailescu
Το μόνο ζεύγος διαδοχικών φυσικών αριθμών που γράφονται ως τέλειες δυνάμεις είναι το (8,9)
https://www.facebook.com/groups/1664980577160670/permalink/3185201775138535
Γεωμετρικές κατασκευές με κανόνα και «σκουριασμένο» διαβήτη !
https://en.wikipedia.org/wiki/Poncelet%E2%80%93Steiner_theorem
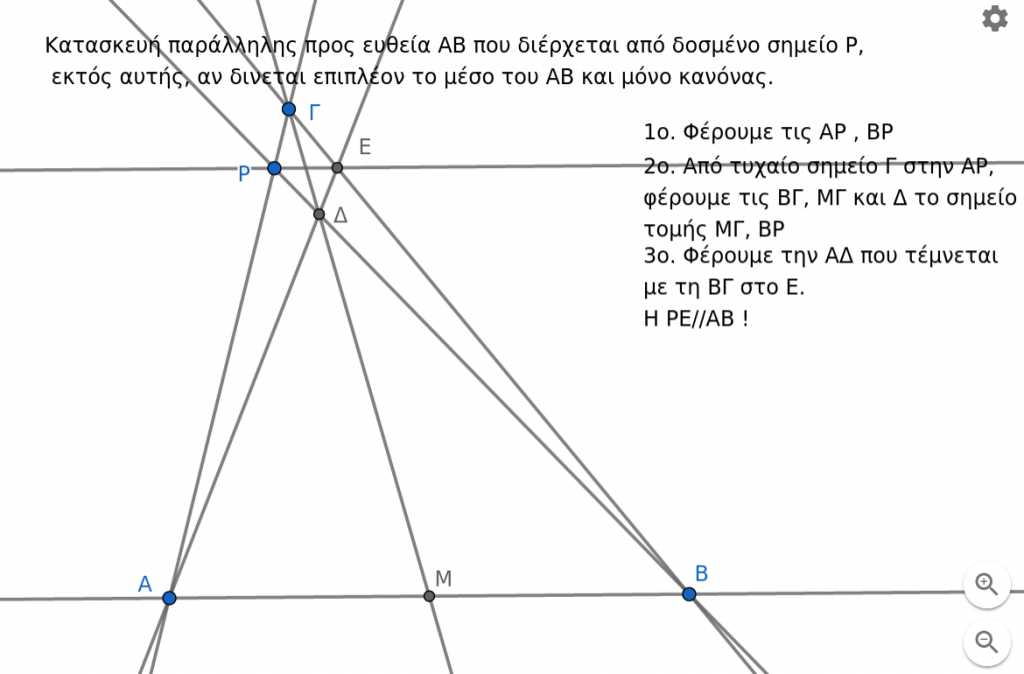
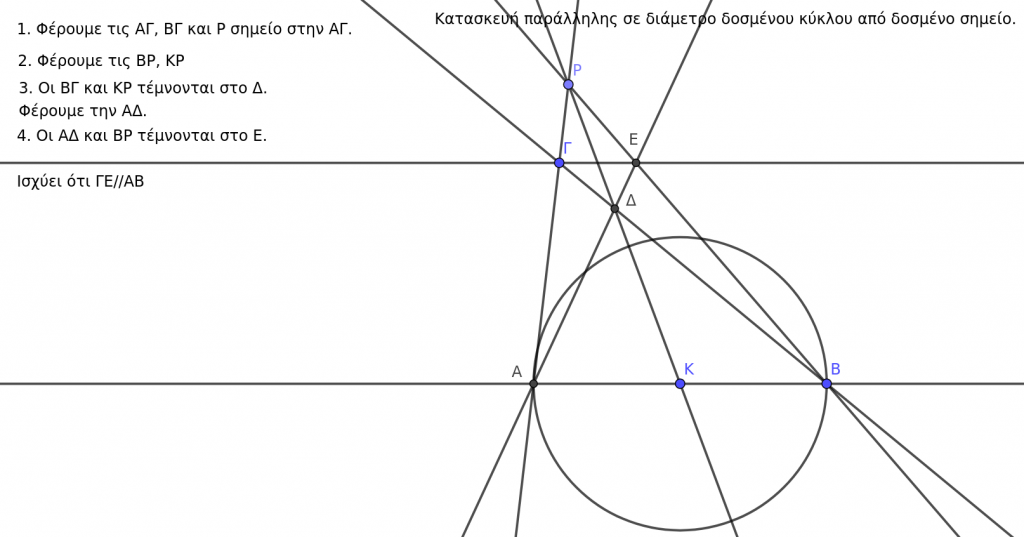
Δείτε την κατασκευή στο παρακάτω gifακι:
https://www.geogebra.org/geometry/mxvcjzuw?embed
https://www.geogebra.org/classic/zzquanan
https://www.geogebra.org/classic/becnhq6t
https://www.geogebra.org/classic/mftdyqv3
The Poncelet-Steiner theorem says
Everything you can construct with a straightedge and a compass you can construct by the straightedge alone, provided you are given a circle and its center.
Motivated by Mascheroni’s result ↑ J.V.Poncelet conjectured this results in 1812��[1]��and it was proved by J.Steiner [2]��in 1833.
It can be shown that the constructions cannot be done by straightedge alone [3] . By the straightedge alone only the so called linear constructions can be done. For instance, using the straightedge alone, without a circle given, is not sufficient to construct square roots. Even simpler constructions as to half a straight line segment are impossible by the straightedge alone. Another example is the result known as Steiner’s theorem:
Steiner’s Theorem: It is impossible to find the center of a given circle with the straightedge alone.
The basic idea of the following proof goes back to Hilbert. If such a construction would be possible, then it would be preserved by projective transformations.��This due to the basic properties of projective transformation which preserve lines, objects constructible by the straightedge. On the other hand, the circle as a conic section is transformed to a conic section in general.��Even worse, the conjugate diameters 1 of a conic section pre-image may not be transformed to the conjugate diameters of the image. Consequently, the center of circle is not projected to the center of the image.
