Κατηγορία: Γεωμετρία Α΄λυκείου
Όλα τα τρίγωνα είναι ίσα μεταξύ τους!
Τετράπλευρο σε τετράπλευρο Διερευνητική εργασία
Τετράπλευρο σε τετράπλευρο Περιγραφή:
Δίνεται το τετράπλευρο ΑΒΓΔ, όπως στο σχήμα.
Αν Ε, Ζ, Η, Θ μέσα των αντιστοίχων πλευρών του, τότε:
α) Βρείτε όσες περισσότερες παρατηρήσεις μπορείτε
β) Αποδείξτε ή απορρίψτε όσες από τις παρατηρήσεις γράψατε στο προηγούμενο ερώτημα.
Γεωμετρική άσκηση
Του Σωκράτη Ρωμανίδη
https://eisatopon.blogspot.com/2022/10/p-q-r-s.html
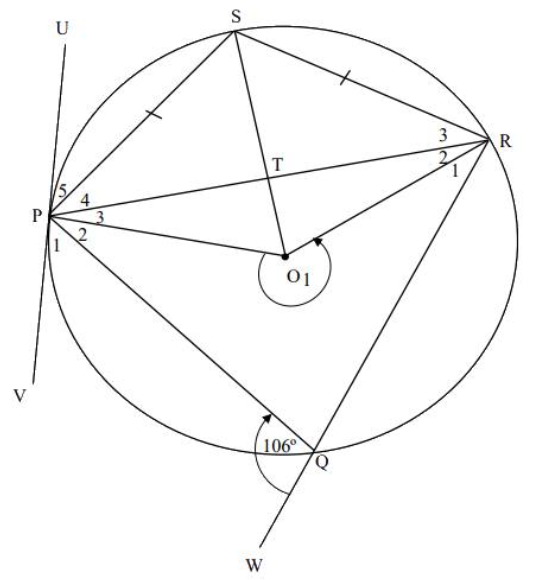
Στο παρακάτω σχήμα τα σημεία \(P, Q, R\) και \(S\) είναι σημεία σε κύκλο με κέντρο Ο. Η ευθεία UV είναι εφαπτομένη στον κύκλο στο σημείο P.Τα τμήματα PR και OS τέμνονται στο T και \( \widehat{PQW} =106^o\) και \( SP =SR \). Να υπολογισθούν οι γωνίες:
i) \( \widehat{PSR} \) ii) \( \widehat{R_3}\) iii) \( \widehat{P_5}\) iv) \( \widehat{O_1} \) v) \( \widehat{P_3}\)
Σταυρόλεξο στα τρίγωνα
202103033252 – Άθροισμα γωνιών – mathematica.gr
https://mathematica.gr/forum/viewtopic.php?p=335262&sid=9d8d03b42738b83dac90f0b1a98d20ff#p335262
Υπάρχει τρίγωνο ώστε το άθροισμα κάθε ζεύγους των γωνιών του να είναι μικρότερο των 120 μοιρών..?
Έστω \(x,y,z\) οι γωνίες ενός τριγώνου, με \(x+y+z=180^o\)
Ας υποθέσουμε ότι για αυτό το τρίγωνο ισχύει ότι το άθροισμα κάθε ζεύγους των γωνιών του είναι μικρότερα των \(120^o\).
Τότε όμως θα πρέπει να είναι
\(x+y<120^o, y+z<120^o, z+x<120^o\)
\( \Rightarrow 2(x+y+z)<360^o\)
\( \Rightarrow x+y+z<180^o \),
προφανώς άτοπο.
Δείτε στον αρχικό σύνδεσμο πολλές ακόμα όμορφες λύσεις!
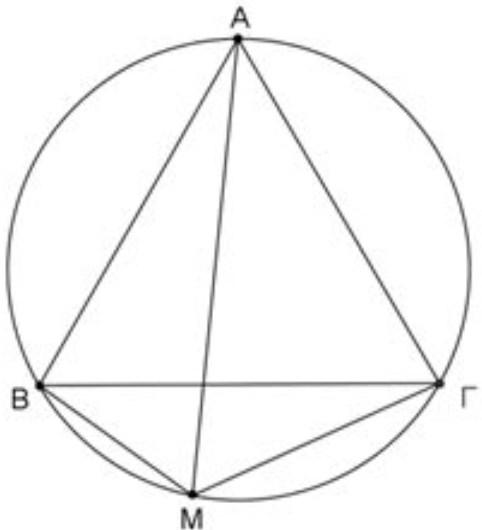
Αποστάσεις σημείου περιγεγραμμένου κύκλου από κορυφές ισοπλεύρου τριγώνου.
Εικοσιδωδεκάεδρο 18 – Ασκήσεις γεωμετρίας Α΄λυκείου 2018
Κατεβάστε από εδώ.
Βιβλία Μαθηματικών – Συνδέσεις για κατέβασμα ή Πληροφορίες: Geometry in figures
Ένα μοναδικό βιβλίο που παρουσιάζει όλες τις ιδιότητες και τη γεωμετρία των διαγωνισμών και όχι μόνο, αποκλειστικά με σχέδια !
Πηγή: Βιβλία Μαθηματικών – Συνδέσεις για κατέβασμα ή Πληροφορίες: Geometry in figures