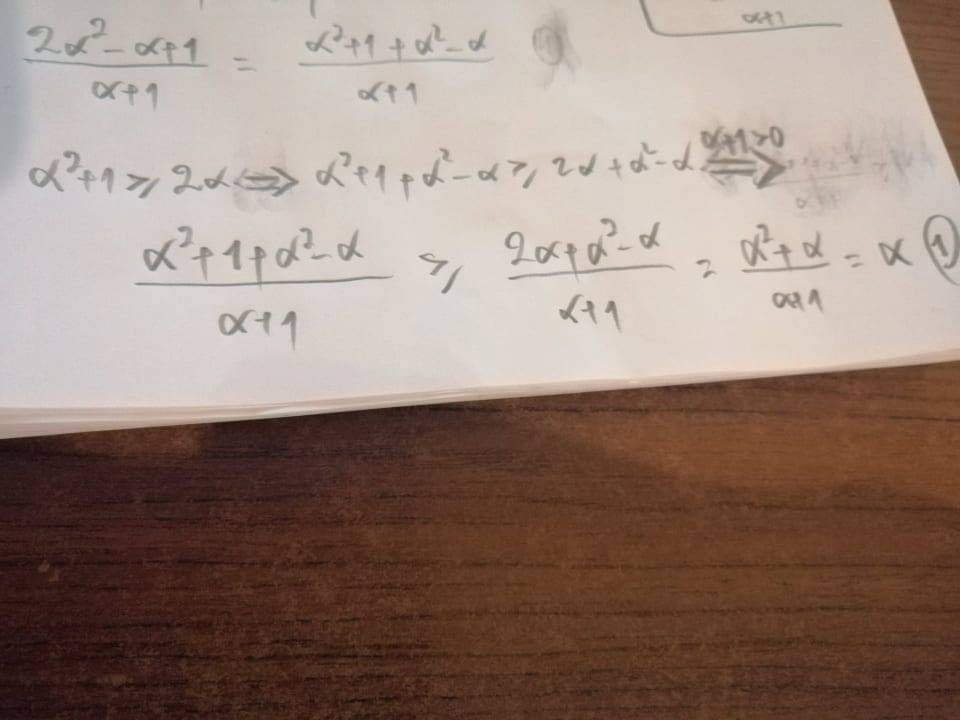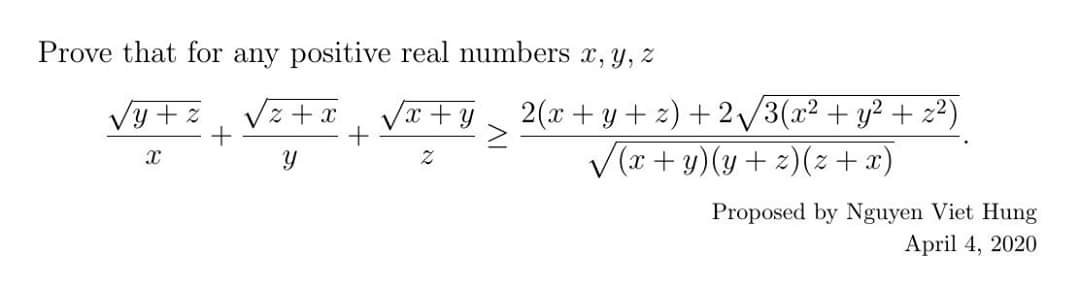Τυπολόγιο Ανισοτήτων ΧΑΣΑΠΗΣ ΣΩΤΗΡΗΣ15731ΦΥΛΛΑΔΙΟ433921573143392%0a
Ετικέτα: Ανισότητες
Ανισότητα Andreescu
![\[\frac{ a_1^2 } { b_1 } + \frac{ a_2 ^2 } { b_2 } + \cdots + \frac{ a_n ^2 } { b_n } \geq \frac{ (a_1 + a_2 + \cdots+ a_n ) ^2 } { b_1 + b_2 + \cdots+ b_n }.\]](https://latex.artofproblemsolving.com/2/6/4/264fff665becc96f5f9e05a178f2a31ee3f2603f.png)
Είναι γνωστή και ως: T2 lemma, Engel’s form, or Sedrakyan’s inequality.
Αναφέρεται και ως Bergstrom’s Inequality με μία απόδειξη:
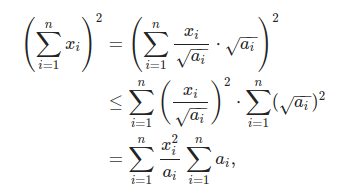
η οποία είναι ισοδύναμη με τη ζητούμενη.
20210406329012-INEQUALITIES THROUGH PROBLEMS Hojoo Lee
Μία διαφορετική απόδειξη της ανισότητας ΑΜ-ΓΜ
The Weighted Arithmetic Mean–Geometric Mean Inequality is Equivalent to the Hölder Inequality
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΝΙΣΟΤΗΤΕΣ – Στεργίου 2017
2020113013251 Μία ανισότητα διαγωνισμών
Ανισότητα
Εικοσιδωδεκάεδρο 21 – Ανισότητες με Ολοκληρώματα
Αγαπητοί φίλοι,
Με ιδιαίτερη χαρά ανακοινώνουμε την κυκλοφορία του 21ου τεύχους του περιοδικού “Εικοσιδωδεκάεδρον” του οποίου την επιμέλεια είχε ο Ροδόλφος Μπόρης και ο Χρήστος Τσιφάκης.

Μπορείτε να τα κατεβάσετε από τη σελίδα http://www.mathematica.gr/icosidodecahedron21.pdf
Η Συντακτική Επιτροπή του περιοδικού