Κατηγορία: Όμιλος Μαθηματικών

Συνάδελφοι, μαθητές και γονείς ελάτε να διαδράσουμε με όμορφα Μαθηματικά Παιχνίδια, Ιστορίες και Θεατρικά
το Σάββατο 5 Απριλίου 2025 ώρα: 09:30 – 14:30 στο 6ο Γυμνάσιο Αθηνών, Ζεύξιδος και Πυθέου, Αθήνα, πλησίον μετρό ΣΥΓΓΡΟΥ-ΦΙΞ.

του πρώην μαθητή του σχολείου Κωνσταντίνου Κριθαρίδη, τον οποίο και ευχαριστούμε πολύ:

https://www.geogebra.org/calculator/ttmkxkws

Η έννοια της παραγώγου για πραγματική συνάρτηση μίας μεταβλητής

Ο λόγος μεταβολής μίας συνάρτησης και η μέση ταχύτητα

Το όριο του λόγου μεταβολής και η στιγμιαία ταχύτητα

Συναρτήσεις πολλών μεταβλητών

Γεωμετρία πραγματικών συναρτήσεων πολλών μεταβλητών

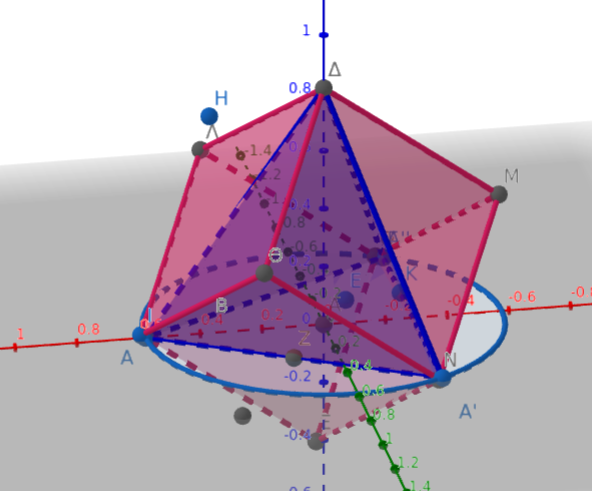
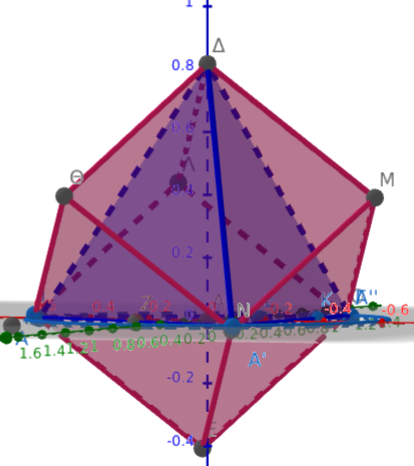
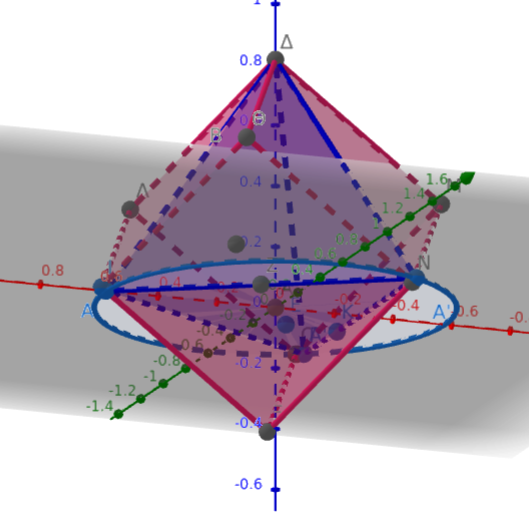
Επιφάνειες δευτέρου βαθμού: https://www.esofia.net/sites/default/files/indicative-capital/ch1.pdf

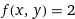
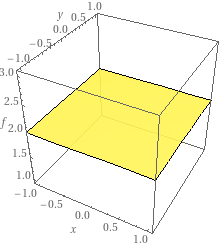
https://www.wolframalpha.com/input?key=&i=f%28x%2Cy%29%3D2

Γενική μορφή επιπέδου z = ax + by +c

https://www.geogebra.org/calculator/bfeauhhf

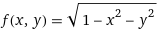
https://www.wolframalpha.com/input?key=&i=f%28x%2Cy%29%3Dsqrt%281-x%5E2+-+y%5E2+%29

https://www.geogebra.org/3d/shfangtz

καμπύλες στάθμης

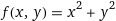
https://www.wolframalpha.com/input?key=&i=f%28x%2Cy%29%3Dx%5E2+%2B+y%5E2

https://www.geogebra.org/m/jccuqfun

https://www.geogebra.org/classic/jccuqfun

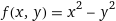
https://www.wolframalpha.com/input?key=&i=f%28x%2Cy%29+%3D+x%5E2+-+y%5E2

https://www.geogebra.org/3d/hdkazcav

Κωνικές τομές

https://www.geogebra.org/3d/da9ks7uw

Ισοϋψείς καμπύλες

Κατευθυνόμενη παράγωγος

Η κατευθυνόμενη παράγωγος στη διεύθυνση ενός διανύσματος u είναι το εσωτερικό γινόμενο της κλίσης grad με το διάνυσμα u

Εύρεση κατεύθυνσης με μέγιστη πτώση…

Αν η κλίση είναι διαφορετική του 0, τότε δείχνει προς εκείνη την κατεύθυνση κατά μήκος της οποίας η συνάρτηση αυξάνεται ταχύτερα.

Ενώ η αντίθετη της κλίσης δείχνει την κατεύθυνση προς την οποία φθίνει γρηγορότερα.

ΕΦαπτόμενο επίπεδο

ΤΟ εφαπτόμενο επίπεδο στο (x0,y0) έχει εξίσωση:

κλίση f(x0,y0) . (x-x0 , y-y0) = 0

Εύρεση ακροτάτων

Δύο κορυφές

https://www.geogebra.org/3d/n326xybq

των συναδέλφων Χρήστου Κυριαζή και Λευτέρη Πρωτοπαπά, από το συνέδριο της ΕΜΕ 2014