Κατηγορία: Όμιλος Μαθηματικών
Πρόβλημα ημέρας Ομίλου Μαθηματικών 11/03/2022
Εξίσωση του Pell, τρίγωνοι και τετραγωνικοί αριθμοί σε νομίσματα
Μάθημα Βασικά στοιχεία στατιστικής μέτρα θέσης και διασποράς κανονική κατανομή.
Θεώρημα Poncelet-Steiner
Γεωμετρικές κατασκευές με κανόνα και «σκουριασμένο» διαβήτη !
https://en.wikipedia.org/wiki/Poncelet%E2%80%93Steiner_theorem
Κατασκευή Παράλληλης από σημείο εκτός ευθείες προς δοσμένη ευθεία ΑΒ με δοσμένο μέσο του ΑΒ
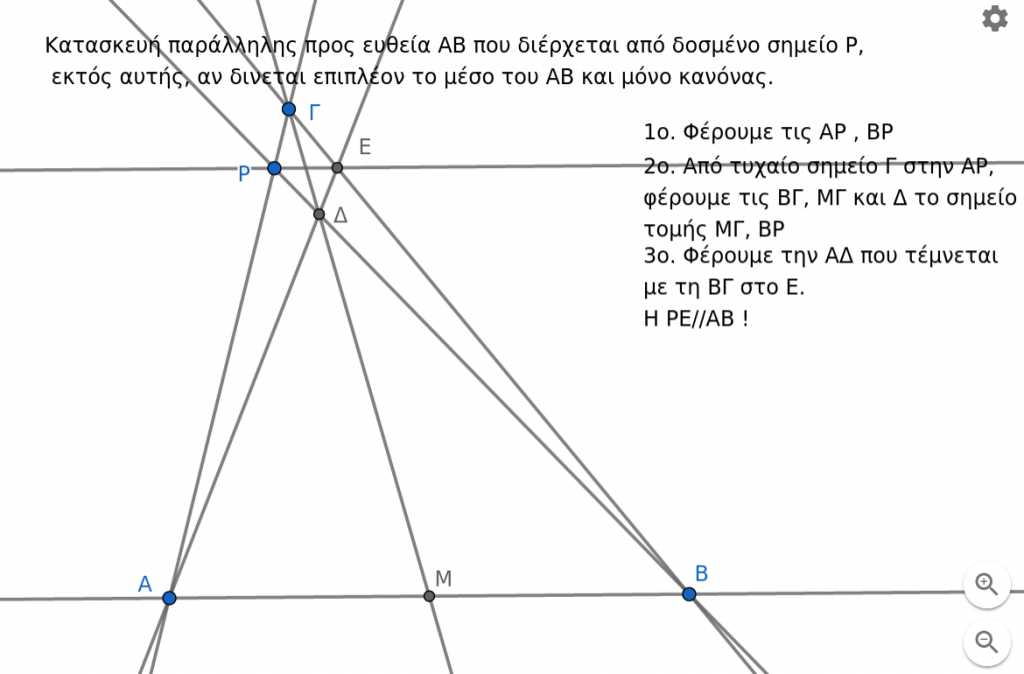
Δείτε την κατασκευή στο παρακάτω gifακι:

https://www.geogebra.org/geometry/mxvcjzuw?embed
Κατασκευή κάθετης προς ευθεία από δοσμένο σημείο.
https://www.geogebra.org/classic/zzquanan

Κατασκευή steiner ευθυγράμμου τμήματος σε δοσμένη ευθεία, με το μέσο του
https://www.geogebra.org/classic/becnhq6t
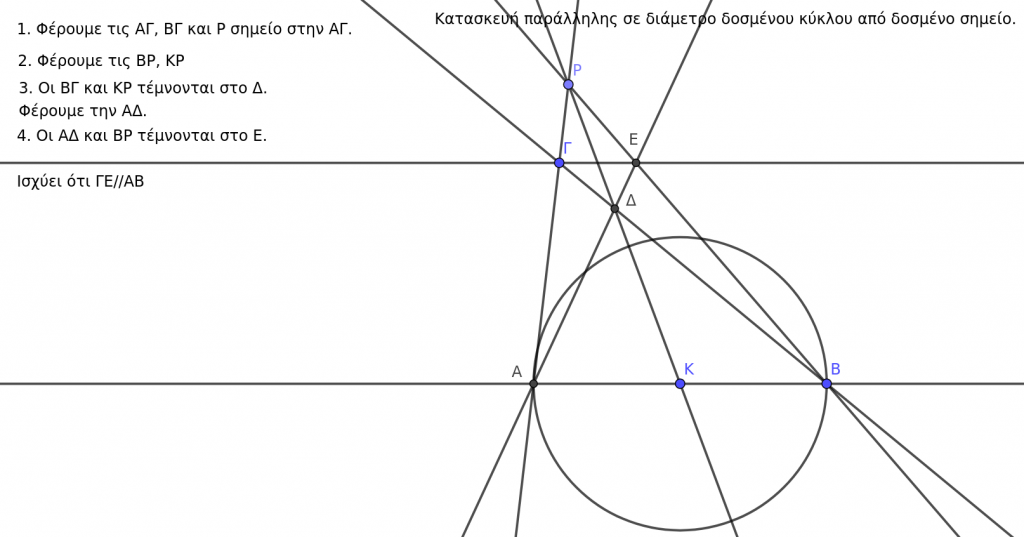
Κατασκευή Steiner παράλληλης από δοσμένο σημείο σε διάμετρο δοσμένου κύκλου.
https://www.geogebra.org/classic/mftdyqv3
The Poncelet-Steiner theorem says
Everything you can construct with a straightedge and a compass you can construct by the straightedge alone, provided you are given a circle and its center.
Motivated by Mascheroni’s result ↑ J.V.Poncelet conjectured this results in 1812��[1]��and it was proved by J.Steiner [2]��in 1833.
It can be shown that the constructions cannot be done by straightedge alone [3] . By the straightedge alone only the so called linear constructions can be done. For instance, using the straightedge alone, without a circle given, is not sufficient to construct square roots. Even simpler constructions as to half a straight line segment are impossible by the straightedge alone. Another example is the result known as Steiner’s theorem:
Steiner’s Theorem: It is impossible to find the center of a given circle with the straightedge alone.
The basic idea of the following proof goes back to Hilbert. If such a construction would be possible, then it would be preserved by projective transformations.��This due to the basic properties of projective transformation which preserve lines, objects constructible by the straightedge. On the other hand, the circle as a conic section is transformed to a conic section in general.��Even worse, the conjugate diameters 1 of a conic section pre-image may not be transformed to the conjugate diameters of the image. Consequently, the center of circle is not projected to the center of the image.
Άρθρο Poncelet-Steiner
33-Poncelet-Steiner-TheoremΕπιπλέον πηγές
2022 ευχές…και ακόμα περισσότερες προσπάθειες
Κάνοντας τετράγωνες τρύπες – Τρίγωνα Reuleaux – Drilling Square Holes – YouTube
A Reuleaux triangle—a shape of constant width—can rotate in a square so that it fills the whole square except little bits in the corners. So, in 1914 Harry James Watts designed a drill bit that can drill a square hole. Here’s a video of the bit in action
Εικασία Collatz
Απολογισμός και υλικό ομίλου Μαθηματικών 2020-21
Ομιλος Αριστείας Μαθηματικών Προτύπου ΓΕΛ Ευαγγελικής σχολής Σμύρνης 2021-22
Όνομα Ομίλου : Όμιλος Αριστείας Μαθηματικών
Υπεύθυνος/νη/νοι καθηγητής/τρια/τες : Σωτήριος Δ. Χασάπης
Ημέρα – ώρα πραγματοποίησης. Πέμπτη 14:30 – 16:00 Θέματα Α΄λυκείου, Παρασκευή 14:30 – 16:00 Προχωρημένα θέματα (συμμετοχή σε τουλάχιστον μία ημέρα).
Μέσω του Ομίλου Μαθηματικών(8ος χρόνος λειτουργίας), οι μαθητές αναμένεται να ζήσουν Μαθηματικές Εμπειρίες, σε όσα το δυνατόν περισσότερα εμπειρικά και νοητικά πλαίσια είναι εφικτό, σε μία ή περισσότερες χρονιές συμμετοχής τους στον όμιλο.
Ενδεικτικά επιδιώκονται:
1) συγκέντρωση και συμπλήρωση γνώσεων από το γυμνάσιο(ειδικά φέτος θα ληφθούν υπόψη οι ιδιαίτερες καταστάσεις που αντιμετώπισαν οι μαθητές τις δύο προηγούμενες σχολικές χρονιές),
2) εφαρμογές Μαθηματικών στην καθημερινή ζωή, ένταξη Μαθηματικών που συναντούν οι μαθητές από τους ίδιους,
3) Μαθηματικά διαγωνισμών και διαγωνισμών Στατιστικής,
4) συμμετοχή σε μαθητικά Μαθηματικά συνέδρια και δράσεις με μετακινήσεις, όπου απαιτηθεί, εφόσον επιτραπεί και ενδεχόμενη συγγραφή και δημοσίευση σχετικών εργασιών των μαθητών.
5) Επίσης, αναπόσπαστο μέρος αποτελούν παιχνίδια, γρίφοι και εφαρμογές σε υπολογιστικά Μαθηματικά.
Σε κάθε περίπτωση επιδιώκεται η ανάπτυξη της Μαθηματικής Εμπειρίας των συμμετεχόντων, μέσω της μεταξύ τους, ενεργούς αλληλεπίδρασης(ο υπεύθυνος καθηγητής έχει το ρόλο συντονιστή που κινητοποιεί τους συμμετέχοντες), για την επίλυση προβλημάτων σε καθένα από τα παραπάνω πλαίσια, η οποία θα υπάρξει χρήσιμη σε κάθε κατάσταση της ακαδημαϊκής τους πορείας, αλλά και της καθημερινότητάς τους.
Ενδεικτικό αναλυτικό πρόγραμμα (αφού αυτό συνδιαμορφώνεται με τους συμμετέχοντες, ανάλογα με τις ανάγκες και τα ενδιαφέροντά τους), καθώς και παραδείγματα από όλα τα παραπάνω μπορείτε να βρείτε στην ιστοσελίδα του ομίλου: omilosmath.blogspot.com ή περισσότερες πληροφορίες στο shasapis@gmail.com.

