Κατηγορία: Γεωμετρία
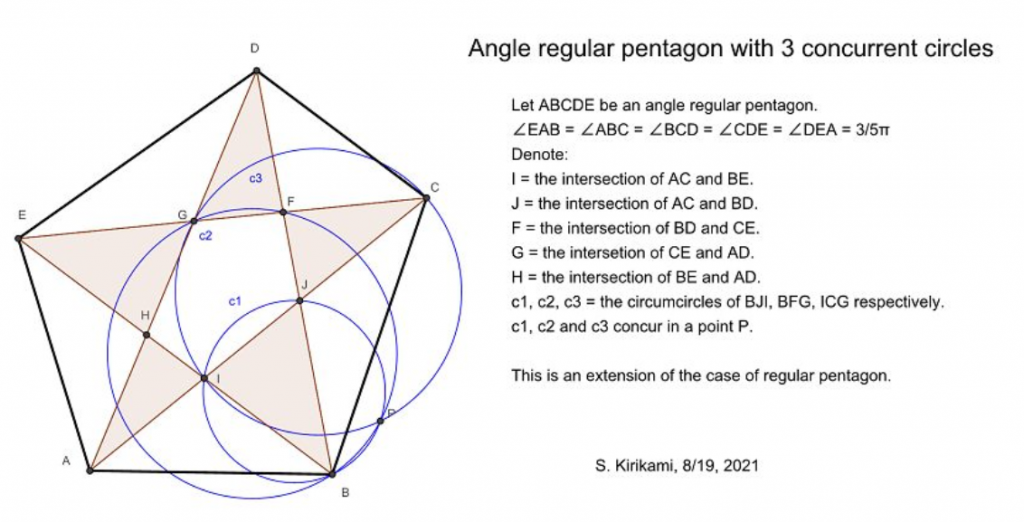
Τρεις συντρέχοντες κύκλοι σε πεντάγωνο
Προβολική γεωμετρία – Ευστάθιος Βασιλείου 2009
Περιοδικό Εκθέτης 23 Η αναγκαιότητα ενίσχυσης της γεωμετρικής σκέψης στην Ελληνική Εκπαίδευση – Γιώργος Ρίζος
Γεωμετρία Θαλής 2020 – Λύσεις – σχολιασμός από τους μαθητές του Ομίλου Μαθηματικών του ΠΛΕΣΣ
Κανονικό δεκαεπτάγωνο Γκουντουβάς
Το κανονικό δεκαεπτάγωνο είναι η πλέον χαρακτηριστική περίπτωση γεωμετρικού προβλήματος το οποίο ΔΕΝ μπόρεσαν να επιλύσουν οι αρχαίοι Έλληνες Γεωμέτρες.
Δηλαδή, ενώ κατασκευάζεται με κανόνα και διαβήτη δεν το κατασκεύασαν. Αυτός που απέδειξε ότι είναι κατασκευάσιμο ήταν ο C. F. Gauss το 1796, ο οποίος έγραψε για αυτό:
“Κάθε αρχάριος στη γεωμετρία γνωρίζει ότι διάφορα κανονικά πολύγωνα μπορούν να κατασκευαστούν με γεωμετρικό τρόπο, και συγκεκριμένα το τρίγωνο, το τετράγωνο, το πεντάγωνο, το δεκαπεντάγωνο και όσα προκύπτουν από αυτά μέσω του επαναλαμβανόμενου διπλασιασμού του αριθμού των πλευρών. Αυτά τα γνώριζαν από την εποχή του Ευκλείδη, και φαίνεται πως είχαν πειστεί από τότε ότι η περιοχή της στοιχειώδους γεωμετρίας δεν μπορούσε να διευρυνθεί… Έτσι μου φαίνεται ακόμη πιο αξιοσημείωτο ότι εκτός από τα συνήθη πολύγωνα υπάρχει ένα σύνολο από άλλα που είναι κατασκευάσιμα με γεωμετρικό τρόπο, π.χ το δεκαεπτάγωνο”.

Πηγή: Facebook